47:
5213:
8865:
5082:). Three types of cones were determined by their vertex angles (measured by twice the angle formed by the hypotenuse and the leg being rotated about in the right triangle). The conic section was then determined by intersecting one of these cones with a plane drawn perpendicular to a generatrix. The type of the conic is determined by the type of cone, that is, by the angle formed at the vertex of the cone: If the angle is acute then the conic is an ellipse; if the angle is right then the conic is a parabola; and if the angle is obtuse then the conic is a hyperbola (but only one branch of the curve).
1792:
1784:
6857:
39:
637:
253:
6141:
31:
382:
7162:) uniquely determine the conic. If another diameter (and its conjugate diameter) are used instead of the major and minor axes of the ellipse, a parallelogram that is not a rectangle is used in the construction, giving the name of the method. The association of lines of the pencils can be extended to obtain other points on the ellipse. The constructions for hyperbolas and parabolas are similar.
5116:
1800:
5149:
commonly used today. Circles, not constructible by the earlier method, are also obtainable in this way. This may account for why
Apollonius considered circles a fourth type of conic section, a distinction that is no longer made. Apollonius used the names 'ellipse', 'parabola' and 'hyperbola' for these curves, borrowing the terminology from earlier Pythagorean work on areas.
4985:, there is a unique conic passing through them, which will be non-degenerate; this is true in both the Euclidean plane and its extension, the real projective plane. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate (reducible, because it contains a line), and may not be unique; see
5735:
3065:
5078:). His work did not survive, not even the names he used for these curves, and is only known through secondary accounts. The definition used at that time differs from the one commonly used today. Cones were constructed by rotating a right triangle about one of its legs so the hypotenuse generates the surface of the cone (such a line is called a
316:). It is usually assumed that the cone is a right circular cone for the purpose of easy description, but this is not required; any double cone with some circular cross-section will suffice. Planes that pass through the vertex of the cone will intersect the cone in a point, a line or a pair of intersecting lines. These are called
3263:
7739:
The solutions to a system of two second degree equations in two variables may be viewed as the coordinates of the points of intersection of two generic conic sections. In particular two conics may possess none, two or four possibly coincident intersection points. An efficient method of locating these
6557:
In the real projective plane, a point conic has the property that every line meets it in two points (which may coincide, or may be complex) and any set of points with this property is a point conic. It follows dually that a line conic has two of its lines through every point and any envelope of lines
6125:
a circle will have the focus-directrix property, but it is still not defined by that property. One must be careful in this situation to correctly use the definition of eccentricity as the ratio of the distance of a point on the circle to the focus (length of a radius) to the distance of that point to
7576:
When viewed from the perspective of the complex projective plane, the degenerate cases of a real quadric (i.e., the quadratic equation has real coefficients) can all be considered as a pair of lines, possibly coinciding. The empty set may be the line at infinity considered as a double line, a (real)
5403:
over any division ring, but in particular over either the real or complex numbers, all non-degenerate conics are equivalent, and thus in projective geometry one speaks of "a conic" without specifying a type. That is, there is a projective transformation that will map any non-degenerate conic to any
5030:
that can be stated as: All mirrors in the shape of a non-degenerate conic section reflect light coming from or going toward one focus toward or away from the other focus. In the case of the parabola, the second focus needs to be thought of as infinitely far away, so that the light rays going toward
2886:
5407:
The three types of conic sections will reappear in the affine plane obtained by choosing a line of the projective space to be the line at infinity. The three types are then determined by how this line at infinity intersects the conic in the projective space. In the corresponding affine space, one
8616:
are classified at each point as elliptic, parabolic, or hyperbolic, accordingly as their second order terms correspond to an elliptic, parabolic, or hyperbolic quadratic form. The behavior and theory of these different types of PDEs are strikingly different – representative examples is that the
6864:
Another method, based on
Steiner's construction and which is useful in engineering applications, is the parallelogram method, where a conic is constructed point by point by means of connecting certain equally spaced points on a horizontal line and a vertical line. Specifically, to construct the
5148:
summarized and greatly extended existing knowledge. Apollonius's study of the properties of these curves made it possible to show that any plane cutting a fixed double cone (two napped), regardless of its angle, will produce a conic according to the earlier definition, leading to the definition
7424:
case of a conic depends on the definition being used and the geometric setting for the conic section. There are some authors who define a conic as a two-dimensional nondegenerate quadric. With this terminology there are no degenerate conics (only degenerate quadrics), but we shall use the more
6106:. Since five points determine a conic, a circle (which may be degenerate) is determined by three points. To obtain the extended Euclidean plane, the absolute line is chosen to be the line at infinity of the Euclidean plane and the absolute points are two special points on that line called the
6550:) as the meet of corresponding rays of two related pencils, it is easy to dualize and obtain the corresponding envelope consisting of the joins of corresponding points of two related ranges (points on a line) on different bases (the lines the points are on). Such an envelope is called a
7341:
points. The intersection possibilities are: four distinct points, two singular points and one double point, two double points, one singular point and one with multiplicity 3, one point with multiplicity 4. If any intersection point has multiplicity > 1, the two curves are said to be
5544:
4379:
7553:, and is thus not normally considered as degenerated. The two lines case occurs when the quadratic expression factors into two linear factors, the zeros of each giving a line. In the case that the factors are the same, the corresponding lines coincide and we refer to the line as a
7307:
in either 2 distinct points (corresponding to two asymptotes) or in 1 double point (corresponding to the axis of a parabola); thus the real hyperbola is a more suggestive real image for the complex ellipse/hyperbola, as it also has 2 (real) intersections with the line at infinity.
620:
is the semi-major axis defined below.) A parabola may also be defined in terms of its focus and latus rectum line (parallel to the directrix and passing through the focus): it is the locus of points whose distance to the focus plus or minus the distance to the line is equal to
491:
A circle is a limiting case and is not defined by a focus and directrix in the
Euclidean plane. The eccentricity of a circle is defined to be zero and its focus is the center of the circle, but its directrix can only be taken as the line at infinity in the projective plane.
8109:
The classification into elliptic, parabolic, and hyperbolic is pervasive in mathematics, and often divides a field into sharply distinct subfields. The classification mostly arises due to the presence of a quadratic form (in two variables this corresponds to the associated
4992:
Four points in the plane in general linear position determine a unique conic passing through the first three points and having the fourth point as its center. Thus knowing the center is equivalent to knowing two points on the conic for the purpose of determining the curve.
7564:
In the real projective plane, since parallel lines meet at a point on the line at infinity, the parallel line case of the
Euclidean plane can be viewed as intersecting lines. However, as the point of intersection is the apex of the cone, the cone itself degenerates to a
3072:
4524:
236:, the apparent difference vanishes: the branches of a hyperbola meet in two points at infinity, making it a single closed curve; and the two ends of a parabola meet to make it a closed curve tangent to the line at infinity. Further extension, by expanding the
5340:
The reflective properties of the conic sections are used in the design of searchlights, radio-telescopes and some optical telescopes. A searchlight uses a parabolic mirror as the reflector, with a bulb at the focus; and a similar construction is used for a
5959:
7440:, when the plane is tangent to the cone (it contains exactly one generator of the cone); or a pair of intersecting lines (two generators of the cone). These correspond respectively to the limiting forms of an ellipse, parabola, and a hyperbola.
3855:
6047:
concepts of
Euclidean geometry (concepts concerned with measuring lengths and angles) can not be immediately extended to the real projective plane. They must be redefined (and generalized) in this new geometry. This can be done for arbitrary
5391:) so that all the lines of a parallel class meet on this line. On the other hand, starting with the real projective plane, a Euclidean plane is obtained by distinguishing some line as the line at infinity and removing it and all its points.
8267:
5289:
construction of the conics and then develops the algebraic equations. This work, which uses Fermat's methodology and
Descartes' notation has been described as the first textbook on the subject. De Witt invented the term 'directrix'.
2651:
2736:
5357:
The conic sections have some very similar properties in the
Euclidean plane and the reasons for this become clearer when the conics are viewed from the perspective of a larger geometry. The Euclidean plane may be embedded in the
3403:
6117:
It has been mentioned that circles in the
Euclidean plane can not be defined by the focus-directrix property. However, if one were to consider the line at infinity as the directrix, then by taking the eccentricity to be
4654:
5037:
concerns the collinearity of three points that are constructed from a set of six points on any non-degenerate conic. The theorem also holds for degenerate conics consisting of two lines, but in that case it is known as
5730:{\displaystyle \left({\begin{matrix}x&y&z\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\z\end{matrix}}\right)=0.}
3060:{\displaystyle {\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}D&E\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+F=0.}
4221:
346:. The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone; for a right cone, this means the cutting plane is perpendicular to the axis. If the cutting plane is
8083:. An oval is a point set that has the following properties, which are held by conics: 1) any line intersects an oval in none, one or two points, 2) at any point of the oval there exists a unique tangent line.
6110:. Lines containing two points with real coordinates do not pass through the circular points at infinity, so in the Euclidean plane a circle, under this definition, is determined by three points that are not
2269:
2121:
3715:
the conic is a parabola and its eccentricity equals 1 (provided it is non-degenerate). Otherwise, assuming the equation represents either a non-degenerate hyperbola or ellipse, the eccentricity is given by
1582:
1188:
4753:
8949:, this solution was rejected by Plato on the grounds that it could not be achieved using only straightedge and compass, however this interpretation of Plutarch's statement has come under criticism.
5864:
4062:
This has precisely one positive solution—the eccentricity— in the case of a parabola or ellipse, while in the case of a hyperbola it has two positive solutions, one of which is the eccentricity.
1771:
1377:
585:
8731:
5529:
4390:
1634:
1240:
6724:
No continuous arc of a conic can be constructed with straightedge and compass. However, there are several straightedge-and-compass constructions for any number of individual points on an arc.
4823:
2186:
7951:
4909:
4060:
3699:
2488:
2426:
8830:
4166:
2856:
227:
422:
is an infinitesimally separated pair of lines. A circle of finite radius has an infinitely distant directrix, while a pair of lines of finite separation have an infinitely distant focus.
8780:
232:
In the
Euclidean plane, the three types of conic sections appear quite different, but share many properties. By extending the Euclidean plane to include a line at infinity, obtaining a
5349:
on La Palma, in the Canary islands, uses a primary parabolic mirror to reflect light towards a secondary hyperbolic mirror, which reflects it again to a focus behind the first mirror.
4213:
3258:{\displaystyle {\begin{pmatrix}x&y&1\end{pmatrix}}{\begin{pmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{pmatrix}}{\begin{pmatrix}x\\y\\1\end{pmatrix}}=0.}
7856:
4005:
1679:
1285:
5103:. His main interest was in terms of measuring areas and volumes of figures related to the conics and part of this work survives in his book on the solids of revolution of conics,
876:
1019:
4834:
2038:
1714:
1320:
6035:
7547:
6558:
with this property is a line conic. At every point of a point conic there is a unique tangent line, and dually, on every line of a line conic there is a unique point called a
7890:
5875:
7301:
7223:
2548:
8869:
8519:
8320:
5218:
4581:
4554:
3722:
8585:
8433:
8362:
4825:
is again the determinant of the 2 × 2 matrix. In the case of an ellipse the squares of the two semi-axes are given by the denominators in the canonical form.
1425:
7491:
5333:
is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. See
800:
6202:
5366:
and define a conic to be the set of points whose coordinates satisfy an irreducible quadratic equation in three variables (or equivalently, the zeros of an irreducible
3316:
2314:
7971:
911:
539:
1106:
833:
516:
8545:
8391:
8051:
8021:
7807:
7780:
7255:
34:
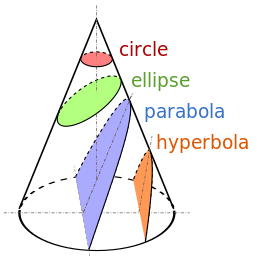
The black boundaries of the colored regions are conic sections. Not shown is the other half of the hyperbola, which is on the unshown other half of the double cone.
7991:
7303:. Thus there is a 2-way classification: ellipse/hyperbola and parabola. Extending the curves to the complex projective plane, this corresponds to intersecting the
6488:
6440:
6411:
6382:
6354:
6325:
6296:
1500:
1475:
6528:
6228:
1447:
1085:
1063:
1041:
8141:
6464:
6268:
6248:
4776:
2562:
6562:. An important theorem states that the tangent lines of a point conic form a line conic, and dually, the points of contact of a line conic form a point conic.
2666:
342:
is a special kind of ellipse, although historically
Apollonius considered it a fourth type. Ellipses arise when the intersection of the cone and plane is a
4849:, a conic section with one focus at the origin and, if any, the other at a negative value (for an ellipse) or a positive value (for a hyperbola) on the
109:
have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the
5974:
As multiplying all six coefficients by the same non-zero scalar yields an equation with the same set of zeros, one can consider conics, represented by
1811:, the focus-directrix property can be used to produce the equations satisfied by the points of the conic section. By means of a change of coordinates (
707:
is the chord between the two vertices: the longest chord of an ellipse, the shortest chord between the branches of a hyperbola. Its half-length is the
8440:
In two variables quadratic forms are classified by discriminant, analogously to conics, but in higher dimensions the more useful classification is as
1944:
hyperbola, one whose asymptotes are perpendicular, there is an alternative standard form in which the asymptotes are the coordinate axes and the line
10542:
7443:
If a conic in the Euclidean plane is being defined by the zeros of a quadratic equation (that is, as a quadric), then the degenerate conics are: the
8026:
intersect each identified line with either one of the two original conics; this step can be done efficiently using the dual conic representation of
6542:
in a projective plane, the dual of each point is a line, and the dual of a locus of points (a set of points satisfying some condition) is called an
3336:
600:
Alternatively, an ellipse can be defined in terms of two focus points, as the locus of points for which the sum of the distances to the two foci is
4590:
323:
and some authors do not consider them to be conics at all. Unless otherwise stated, "conic" in this article will refer to a non-degenerate conic.
9565:
From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren
7179:, ellipses and hyperbolas are not distinct: one may consider a hyperbola as an ellipse with an imaginary axis length. For example, the ellipse
3578:
of the 2 × 2 matrix) are invariant under arbitrary rotations and translations of the coordinate axes, as is the determinant of the
9958:
Wilczynski, E. J. (1916), "Some remarks on the historical development and the future prospects of the differential geometry of plane curves",
8613:
7447:, a point, or a pair of lines which may be parallel, intersect at a point, or coincide. The empty set case may correspond either to a pair of
4374:{\displaystyle {\frac {{\tilde {x}}^{2}}{-S/(\lambda _{1}^{2}\lambda _{2})}}+{\frac {{\tilde {y}}^{2}}{-S/(\lambda _{1}\lambda _{2}^{2})}}=1,}
50:
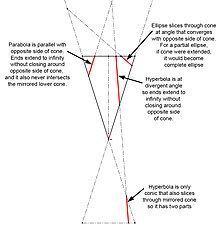
This diagram clarifies the different angles of the cutting planes that result in the different properties of the three types of conic section.
7719:) in a plane and the system of conics which pass through a fixed set of four points (again in a plane and no three collinear) is called a
8596:
5408:
obtains an ellipse if the conic does not intersect the line at infinity, a parabola if the conic intersects the line at infinity in one
5374:, and the irreducible quadrics in a two dimensional projective space (that is, having three variables) are traditionally called conics.
7584:
To distinguish the degenerate cases from the non-degenerate cases (including the empty set with the latter) using matrix notation, let
5412:
corresponding to the axis, and a hyperbola if the conic intersects the line at infinity in two points corresponding to the asymptotes.
2197:
2049:
10965:
6504:) is uniquely determined by prescribing the images of three lines, for the Steiner generation of a conic section, besides two points
1513:
1119:
288:
The conic sections have been studied for thousands of years and have provided a rich source of interesting and beautiful results in
8591:
every surface can be taken to be globally (at every point) positively curved, flat, or negatively curved. In higher dimensions the
5265:
to the study of conics. This had the effect of reducing the geometrical problems of conics to problems in algebra. However, it was
9645:
7365:. Intersecting with the line at infinity, each conic section has two points at infinity. If these points are real, the curve is a
10337:
8633:
7741:
4662:
2878:
7727:
of the pencil. Through any point other than a base point, there passes a single conic of the pencil. This concept generalizes a
10514:
11057:
10694:
10654:
10535:
10345:
10323:
10204:
10184:
10161:
10139:
9629:
9597:
9572:
6063:. Several metrical concepts can be defined with reference to these choices. For instance, given a line containing the points
5753:
5247:
and this helped to provide impetus for the study of this new field. In particular, Pascal discovered a theorem known as the
5162:
AD) is credited with expounding on the importance of the concept of a conic's focus, and detailing the related concept of a
4519:{\displaystyle {\frac {{\tilde {x}}^{2}}{-S/(\lambda _{1}\Delta )}}+{\frac {{\tilde {y}}^{2}}{-S/(\lambda _{2}\Delta )}}=1,}
7428:
In the Euclidean plane, using the geometric definition, a degenerate case arises when the cutting plane passes through the
1720:
1326:
544:
8680:
5430:
590:
8857:
1588:
1194:
11123:
10745:
10644:
10445:
5275:
who first defined the conic sections as instances of equations of second degree. Written earlier, but published later,
1816:
4785:
2132:
11153:
11113:
10471:
10453:
10423:
10385:
10365:
10256:
10227:
10059:
9483:
9173:
8841:
7895:
6530:
only the images of 3 lines have to be given. These 5 items (2 points, 3 lines) uniquely determine the conic section.
4861:
4013:
3612:
2440:
2378:
10823:
10528:
9546:
8785:
7751:
The procedure to locate the intersection points follows these steps, where the conics are represented by matrices:
7321:
7165:
Yet another general method uses the polarity property to construct the tangent envelope of a conic (a line conic).
5370:). More technically, the set of points that are zeros of a quadratic form (in any number of variables) is called a
4082:
3267:
This form is a specialization of the homogeneous form used in the more general setting of projective geometry (see
6052:, but to obtain the real projective plane as the extended Euclidean plane, some specific choices have to be made.
2770:
144:
9530:
9257:
8674:
6729:
if the points of intersection of opposite sides of a hexagon are collinear, then the six vertices lie on a conic.
6576:
10004:
Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review
8735:
8086:
Generalizing the focus properties of conics to the case where there are more than two foci produces sets called
10970:
10891:
10881:
10818:
10213:
8853:
7320:: the non-degenerate conics cannot be distinguished from one another, since any can be taken to any other by a
5049:". This is important for many applications, such as aerodynamics, where a smooth surface is required to ensure
4174:
17:
7812:
1812:
10568:
10131:
8864:
8609:
8127:
7728:
7712:
7140:
projectively but not perspectively. The sought for conic is obtained by this construction since three points
6539:
6084:
5174:
Apollonius's work was translated into Arabic, and much of his work only survives through the Arabic version.
4974:
495:
The eccentricity of an ellipse can be seen as a measure of how far the ellipse deviates from being circular.
7706:
5362:
and the conics may be considered as objects in this projective geometry. One way to do this is to introduce
3881:
11163:
10788:
10684:
1640:
1246:
5015:
of a conic. A point on just one tangent line is on the conic. A point on no tangent line is said to be an
839:
11047:
11011:
10710:
10623:
6107:
5039:
3524:
are polynomial coefficients, in contrast to some sources that denote the semimajor and semiminor axes as
2749:
1808:
970:
7892:
which correspond to the degenerate conic of the pencil. This can be done by imposing the condition that
2339:-axis only (for the parabola). The rectangular hyperbola, however, is instead symmetric about the lines
1987:
1685:
1291:
11168:
11021:
10659:
8897:
7558:
7334:
6008:
5954:{\displaystyle M=\left({\begin{matrix}A&B&D\\B&C&E\\D&E&F\end{matrix}}\right),}
5346:
450:
386:
125:
7500:
5230:
5212:
11158:
11067:
9475:
9431:
7863:
6356:. Then the intersection points of corresponding lines form a non-degenerate projective conic section.
5099:
BC) is known to have studied conics, having determined the area bounded by a parabola and a chord in
3850:{\displaystyle e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}},}
717:). When an ellipse or hyperbola are in standard position as in the equations below, with foci on the
4986:
648:), foci, and directrix, various geometric features and lengths are associated with a conic section.
10980:
10960:
10896:
10813:
10715:
10674:
8936:
The empty set is included as a degenerate conic, since it may arise as a solution of this equation.
8592:
7550:
7350:. If there is only one intersection point, which has multiplicity 4, the two curves are said to be
7312:
7260:
7182:
6605:
6546:
of lines. Using Steiner's definition of a conic (this locus of points will now be referred to as a
2502:
10287:
8640:
8481:
8284:
5201:
5115:
4559:
4532:
11148:
10871:
10679:
9297:
8887:
8882:
8550:
8398:
8327:
8080:
6769:
that lies on this line and is on the conic determined by the five points can be constructed. Let
5421:
5363:
4978:
4846:
1390:
7454:
5139:
3704:
the eccentricity can be written as a function of the coefficients of the quadratic equation. If
1799:
773:
10664:
8835:
8588:
8069:
7578:
6163:
5175:
3575:
3282:
2280:
1791:
1783:
10778:
10097:
9518:
9037:
7956:
7346:. If there is an intersection point of multiplicity at least 3, the two curves are said to be
7338:
6856:
884:
521:
11042:
10740:
10689:
10578:
10077:
10051:
10044:
10015:
9898:
9858:
9767:
9621:
9550:
9180:
9029:
8907:
8845:
8463:
7400:. If the coefficients of a conic section are real, the points at infinity are either real or
6152:(coordinate-free) approach to defining the conic sections in a projective plane was given by
5359:
3507:
2658:
1091:
8599:
are interesting objects of study, and have strikingly different properties, as discussed at
8452:(mix of positive and negative but no zeros). This classification underlies many that follow.
806:
501:
11118:
10990:
10649:
9272:
8849:
8523:
8369:
8029:
7999:
7785:
7758:
7228:
6618:
5535:
5342:
5248:
5152:
5075:
4962:
426:
Alternatively, one can define a conic section purely in terms of plane geometry: it is the
10901:
8971:
Consider finding the midpoint of a line segment with one endpoint on the line at infinity.
8262:{\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{k}^{2}-x_{k+1}^{2}-\cdots -x_{k+\ell }^{2},}
7976:
6473:
6416:
6387:
6367:
6330:
6301:
6281:
5869:(or some variation of this) so that the matrix of the conic section has the simpler form,
2646:{\displaystyle (a\sec \theta ,b\tan \theta ),{\text{ or }}(\pm a\cosh \psi ,b\sinh \psi )}
1481:
1456:
593:
are the same as those obtained by planes intersecting a cone is facilitated by the use of
8:
10955:
10833:
10798:
10755:
10735:
10170:
9510:
9498:
9033:
8600:
8475:
7566:
6507:
6207:
5244:
5128:
5034:
2753:
2363:
1431:
1069:
1047:
1025:
655:
is the line joining the foci of an ellipse or hyperbola, and its midpoint is the curve's
427:
347:
99:
75:
10248:
Practical Conic Sections: The geometric properties of ellipses, parabolas and hyperbolas
9315:
7361:
intersects each conic section twice. If the intersection point is double, the line is a
6587:(1847) as part of his attempt to remove all metrical concepts from projective geometry.
2731:{\displaystyle \left(dt,{\frac {d}{t}}\right),{\text{ where }}d={\frac {c}{\sqrt {2}}}.}
350:
to exactly one generating line of the cone, then the conic is unbounded and is called a
11085:
10876:
10856:
10669:
10438:
10011:
9652:
9302:
Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions
8912:
8471:
8459:
8055:
the points of intersection will represent the solutions to the initial equation system.
6449:
6253:
6233:
6149:
5088:(fl. 300 BC) is said to have written four books on conics but these were lost as well.
4761:
2757:
366:
289:
138:
94:
is a special case of the ellipse, though it was sometimes called as a fourth type. The
10828:
8980:
Coxeter and several other authors use the term 'self-conjugate' instead of 'absolute'.
8130:, namely by their positive index, zero index, and negative index: a quadratic form in
3279:
The conic sections described by this equation can be classified in terms of the value
2764:), and all conic sections arise in this way. The most general equation is of the form
10985:
10932:
10803:
10618:
10613:
10497:
10467:
10449:
10419:
10403:
10381:
10361:
10341:
10319:
10312:
10289:
Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes
10252:
10223:
10200:
10180:
10157:
10135:
10055:
10028:
10007:
9625:
9593:
9568:
9514:
9479:
9169:
8467:
8087:
7448:
7401:
5388:
5262:
5166:, including the case of the parabola (which is lacking in Apollonius's known works).
130:
110:
95:
10416:
Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry
9972:
5967:
If the determinant of the matrix of the conic section is zero, the conic section is
5254:
5233:", a precursor to the concept of limits. Kepler first used the term 'foci' in 1604.
881:
For conics in standard position, these parameters have the following values, taking
628:; plus if the point is between the directrix and the latus rectum, minus otherwise.
10975:
10861:
10838:
9967:
8618:
7745:
7433:
7415:
7347:
7304:
6571:
6049:
6003:
5400:
5384:
5334:
5236:
5194:
3408:
678:
594:
440:
301:
233:
115:
10500:
9830:
8072:
2, as some formulas can not be used. For example, the matrix representations used
6126:
the directrix (this distance is infinite) which gives the limiting value of zero.
5178:
found applications of the theory, most notably the Persian mathematician and poet
3875:
It can also be shown that the eccentricity is a positive solution of the equation
11090:
10906:
10848:
10750:
10573:
10552:
10375:
10355:
10246:
10217:
10194:
10174:
9999:
9469:
9425:
9237:
9163:
8917:
8902:
8892:
8466:
describes the infinitesimal geometry, and may at each point be either positive –
8098:
7590:
be the determinant of the 3 × 3 matrix of the conic section—that is,
5226:
5183:
4982:
709:
370:
309:
134:
106:
71:
38:
6102:
A conic in a projective plane that contains the two absolute points is called a
5179:
5079:
4071:
10773:
10598:
10583:
10560:
10399:
10307:
9613:
9243:
8364:– positive-definite (the negative is also included), corresponding to ellipses,
8121:
6690:
6672:
5367:
5330:
241:
8962:
This form of the equation does not generalize to fields of characteristic two.
3398:{\displaystyle \left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|.}
681:
parallel to the directrix and passing through a focus; its half-length is the
11142:
11105:
10886:
10866:
10588:
10520:
10433:
10089:
8626:
8622:
8135:
8065:
7662:
be the discriminant. Then the conic section is non-degenerate if and only if
7437:
7378:
7358:
6713:
6501:
6446:(1-1 correspondence) such that corresponding lines intersect on a fixed line
6275:
6153:
6135:
6055:
Fix an arbitrary line in a projective plane that shall be referred to as the
5258:
5240:
5127:
The greatest progress in the study of conics by the ancient Greeks is due to
4649:{\displaystyle \left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)}
760:
as in the standard equation below. By analogy, for a hyperbola the parameter
415:
10279:
The Universe of Conics: From the ancient Greeks to 21st century developments
5197:
and cubic equations, although his solution did not deal with all the cases.
11052:
11026:
11016:
11006:
10808:
10628:
10149:
9502:
8111:
7362:
6271:
6044:
5409:
5200:
An instrument for drawing conic sections was first described in 1000 AD by
5050:
5012:
4965:; for instance, determining the orbits of objects revolving about the Sun.
3319:
721:-axis and center at the origin, the vertices of the conic have coordinates
343:
607:; while a hyperbola is the locus for which the difference of distances is
369:(intersection of a plane with a sphere, producing a circle or point), and
46:
10927:
10765:
10265:
8677:
as elliptic, parabolic, or hyperbolic accordingly as their half-trace is
8094:
7569:, i.e. with the apex at infinity. Other sections in this case are called
6972:
equal segments and use parallel projection, with respect to the diagonal
5276:
5266:
5070:
It is believed that the first definition of a conic section was given by
3551:
3331:
2862:
1827:-axis as principal axis and the origin (0,0) as center. The vertices are
237:
8277:, is the negative index, and the remaining variables are the zero index
6853:, as many additional points on the conic as desired can be constructed.
5019:(or inner point) of the conic, while a point on two tangent lines is an
229:
The geometric properties of the conic can be deduced from its equation.
10922:
9542:
8478:; infinitesimally, to second order the surface looks like the graph of
8079:
A generalization of a non-degenerate conic in a projective plane is an
6579:
defined a conic as the point set given by all the absolute points of a
6059:. Select two distinct points on the absolute line and refer to them as
5286:
5190:
5089:
5071:
5054:
5046:
4584:
636:
252:
244:
coordinates, provides the means to see this unification algebraically.
137:
of degree 2; that is, as the set of points whose coordinates satisfy a
129:. The type of conic is determined by the value of the eccentricity. In
9304:, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866), p. 203.
10783:
10505:
7716:
7573:. The non-degenerate cylindrical sections are ellipses (or circles).
7444:
7366:
7333:, two conic sections have four points in common (if one accounts for
6608:
6443:
6111:
5318:
5311:
3489:
2554:
1933:. In standard form the parabola will always pass through the origin.
1506:
389:
sharing a focus point and directrix line, including an ellipse (red,
335:
281:
79:
8840:
The variance-to-mean ratio classifies several important families of
7429:
6140:
8946:
7374:
6712:
A von Staudt conic in the real projective plane is equivalent to a
6662:
6583:
that has absolute points. Von Staudt introduced this definition in
5307:
3471:
2494:
1383:
748:
is the shortest diameter of an ellipse, and its half-length is the
331:
274:
113:
of those points whose distances to some particular point, called a
83:
8872:, move left and right over the SVG image to rotate the double cone
7809:, consider the pencil of conics given by their linear combination
7549:
An imaginary ellipse does not satisfy the general definition of a
6727:
One of them is based on the converse of Pascal's theorem, namely,
11095:
11080:
8646:
8322:
In two variables the non-zero quadratic forms are classified as:
7370:
7343:
5747:
Some authors prefer to write the general homogeneous equation as
5371:
5326:
5303:
3427:
2432:
1112:
327:
267:
87:
30:
10407:
7993:. These turn out to be the solutions of a third degree equation.
6709:) of a polarity is one which is incident with its polar (pole).
2264:{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,}
2116:{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}
11075:
10193:
Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999),
9538:
8660:
8023:, identify the two, possibly coincident, lines constituting it.
7397:
5299:
5085:
3550:
of the conic section's quadratic equation (or equivalently the
3451:
2370:
1894:
1577:{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
1183:{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
963:
700:) is the distance from a focus to the corresponding directrix.
381:
339:
260:
91:
4833:
10094:
Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry
7561:
2) and this is the previous case of a tangent cutting plane.
5322:
5298:
For specific applications of each type of conic section, see
5074:(died 320 BC) as part of his solution of the Delian problem (
2760:
in two variables is always a conic section (though it may be
764:
in the standard equation is also called the semi-minor axis.
498:
If the angle between the surface of the cone and its axis is
373:(intersection of an elliptic cone with a concentric sphere).
362:
halves of the cone, producing two separate unbounded curves.
67:
9242:(Mineola, NY: Dover, 2007). Originally published in 1957 by
6500:
As a projective mapping in a projective plane over a field (
4171:
can be converted to canonical form in transformed variables
2333:-axis (for the circle, ellipse and hyperbola), or about the
418:
circle centered at the focus, and the conic of eccentricity
8064:
Conics may be defined over other fields (that is, in other
5251:
from which many other properties of conics can be deduced.
4961:
The polar form of the equation of a conic is often used in
4748:{\displaystyle \lambda ^{2}-(A+C)\lambda +(AC-(B/2)^{2})=0}
2321:
The first four of these forms are symmetric about both the
1911:. For the parabola, the standard form has the focus on the
10277:
Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016),
8844:: the constant distribution as circular (eccentricity 0),
7132:. The labeling associates the lines of the pencil through
5000:
points in general position that it passes through and 5 –
1778:
7436:, when the plane intersects the cone only at the apex; a
4996:
Furthermore, a conic is determined by any combination of
10515:
Occurrence of the conics. Conics in nature and elsewhere
9255:
Ayoub, Ayoub B., "The eccentricity of a conic section",
6129:
5383:
is embedded in the real projective plane by adjoining a
3601:
2883:
The above equation can be written in matrix notation as
518:
and the angle between the cutting plane and the axis is
9827:
Jacob Steiner's Vorlesungen über synthetische Geometrie
9590:
A History of Algebra: From al-Khwārizmī to Emmy Noether
8068:). However, some care must be used when the field has
6144:
Definition of the Steiner generation of a conic section
300:
A conic is the curve obtained as the intersection of a
98:
studied conic sections, culminating around 200 BC with
10495:
10448:(Readings in Mathematics), New York: Springer-Verlag,
9567:. Springer Science & Business Media. p. 110.
9471:
Science in Medieval Islam: An Illustrated Introduction
9270:
Ayoub, A. B., "The central conic sections revisited",
8273:
is the positive index, the number of −1 coefficients,
6497:
mapping is a finite sequence of perspective mappings.
5890:
5859:{\displaystyle Ax^{2}+2Bxy+Cy^{2}+2Dxz+2Eyz+Fz^{2}=0,}
5693:
5582:
5553:
5163:
4599:
3345:
3221:
3110:
3081:
3024:
3000:
2971:
2919:
2895:
1954:
is the principal axis. The foci then have coordinates
1823:. For ellipses and hyperbolas a standard form has the
10276:
9592:. Springer Science & Business Media. p. 29.
8788:
8738:
8683:
8553:
8526:
8484:
8401:
8372:
8330:
8287:
8144:
8032:
8002:
7979:
7959:
7898:
7866:
7815:
7788:
7761:
7711:
A (non-degenerate) conic is completely determined by
7503:
7457:
7263:
7231:
7185:
6510:
6476:
6452:
6419:
6390:
6370:
6333:
6304:
6284:
6256:
6236:
6210:
6166:
6011:
5878:
5756:
5547:
5433:
5011:
Any point in the plane is on either zero, one or two
4864:
4837:
Development of the conic section as the eccentricity
4788:
4764:
4665:
4593:
4562:
4535:
4393:
4224:
4177:
4085:
4076:
In the case of an ellipse or hyperbola, the equation
4016:
3884:
3725:
3615:
3339:
3285:
3075:
2889:
2773:
2669:
2565:
2505:
2443:
2381:
2283:
2200:
2135:
2052:
1990:
1723:
1688:
1643:
1591:
1516:
1484:
1459:
1434:
1393:
1329:
1294:
1249:
1197:
1122:
1094:
1072:
1050:
1028:
973:
887:
842:
809:
776:
547:
524:
504:
147:
8858:
cumulants of some discrete probability distributions
6039:
5243:
developed a theory of conics using an early form of
1766:{\displaystyle {\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}}
1372:{\displaystyle {\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}}
580:{\displaystyle {\frac {\cos \alpha }{\cos \beta }}.}
376:
10394:Protter, Murray H.; Morrey, Charles B. Jr. (1970),
9190:
9188:
8726:{\displaystyle 0\leq |\operatorname {tr} |/2<1,}
8101:, which shares many properties with planar conics.
7425:traditional terminology and avoid that definition.
7026:label the left-hand endpoints of the segments with
5524:{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}=0.}
3606:When the conic section is written algebraically as
10437:
10311:
10043:
9829:, B. G. Teubner, Leipzig 1867 (from Google Books:
9563:Sidoli, Nathan; Brummelen, Glen Van (2013-10-30).
8824:
8774:
8725:
8579:
8539:
8513:
8427:
8385:
8356:
8314:
8261:
8045:
8015:
7985:
7965:
7945:
7884:
7850:
7801:
7774:
7541:
7485:
7295:
7249:
7217:
7168:
6522:
6482:
6458:
6434:
6405:
6376:
6348:
6319:
6290:
6262:
6242:
6222:
6196:
6029:
5953:
5858:
5729:
5523:
5325:of two massive objects that interact according to
5189:A century before the more famous work of Khayyam,
4977:. Formally, given any five points in the plane in
4903:
4817:
4770:
4747:
4648:
4575:
4548:
4518:
4373:
4207:
4160:
4054:
3999:
3849:
3693:
3564:of the 2 × 2 matrix) and the quantity
3397:
3310:
3257:
3059:
2850:
2730:
2645:
2542:
2482:
2420:
2308:
2263:
2180:
2115:
2032:
1765:
1708:
1673:
1629:{\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}
1628:
1576:
1494:
1469:
1441:
1419:
1371:
1314:
1279:
1235:{\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}
1234:
1182:
1100:
1079:
1057:
1035:
1013:
905:
870:
827:
794:
670:) is the distance between the center and a focus.
579:
533:
510:
221:
141:in two variables which can be written in the form
10192:
9986:
9715:
9339:
9285:
9149:
9089:
9077:
9061:
9012:
8126:Quadratic forms over the reals are classified by
3268:
11140:
10125:
9945:
9185:
8104:
7899:
7683:, two parallel lines (possibly coinciding) when
6860:Parallelogram method for constructing an ellipse
4973:Just as two (distinct) points determine a line,
4818:{\displaystyle \Delta =\lambda _{1}\lambda _{2}}
2181:{\displaystyle y^{2}=4ax,{\text{ with }}a>0,}
10466:(fifth ed.), Addison-Wesley, p. 434,
9646:"Apollonius of Perga Conics Books One to Seven"
9562:
7946:{\displaystyle \det(\lambda C_{1}+\mu C_{2})=0}
7432:of the cone. The degenerate conic is either: a
5964:but this notation is not used in this article.
5352:
4904:{\displaystyle r={\frac {l}{1+e\cos \theta }},}
4065:
10550:
10413:
10109:
9699:
9697:
9434:(Cambridge: Cambridge University Press, 2013).
5031:or coming from the second focus are parallel.
4055:{\displaystyle \Delta =AC-{\frac {B^{2}}{4}}.}
3694:{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,\,}
2483:{\displaystyle (a\cos \theta ,b\sin \theta ),}
2421:{\displaystyle (a\cos \theta ,a\sin \theta ),}
10536:
10393:
9535:Geometry and Algebra in Ancient Civilizations
9194:
9137:
9113:
9101:
8832:mirroring the classification by eccentricity.
8825:{\displaystyle |\operatorname {tr} |/2>1,}
8393:– degenerate, corresponding to parabolas, and
7581:and the other cases as previously mentioned.
7373:; if there is only one double point, it is a
7369:; if they are imaginary conjugates, it is an
5740:The 3 × 3 matrix above is called
5065:
4161:{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,}
589:A proof that the above curves defined by the
10479:
10461:
10360:(2nd ed.), Edinburgh: Oliver and Boyd,
9620:(3rd ed.). New York: Springer. p.
9206:
9125:
9049:
8114:), but can also correspond to eccentricity.
7707:Pencil (mathematics) § Pencil of conics
5182:, who found a geometrical method of solving
3069:The general equation can also be written as
2851:{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}
222:{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}
10462:Thomas, George B.; Finney, Ross L. (1979),
9694:
9165:Math refresher for scientists and engineers
8597:manifolds with constant sectional curvature
8073:
7257:geometrically a complex rotation, yielding
7225:becomes a hyperbola under the substitution
5394:
5280:
5270:
5229:extended the theory of conics through the "
3322:of the equation. Thus, the discriminant is
78:. The three types of conic section are the
10543:
10529:
10484:(Revised ed.), D.C. Heath and Company
10314:A History of Mathematics / An Introduction
9957:
9026:Precalculus: With Unit Circle Trigonometry
8775:{\displaystyle |\operatorname {tr} |/2=1,}
8435:– indefinite, corresponding to hyperbolas.
7734:
6565:
5415:
5045:Non-degenerate conic sections are always "
640:Conic parameters in the case of an ellipse
42:Conic sections visualized with torch light
9971:
9796:
9612:
9588:Waerden, Bartel L. van der (2013-06-29).
8645:Real Möbius transformations (elements of
7451:parallel lines such as with the equation
4656:— that is, the solutions of the equation
4208:{\displaystyle {\tilde {x}},{\tilde {y}}}
4157:
3690:
2743:
1923:and the directrix the line with equation
1491:
1466:
1438:
1416:
1076:
1054:
1032:
1010:
354:. In the remaining case, the figure is a
10373:
10353:
10318:(2nd ed.), Addison Wesley Longman,
10073:
10041:
9894:
9854:
9814:
9763:
9751:
9313:
9232:
9230:
9228:
8863:
7851:{\displaystyle \lambda C_{1}+\mu C_{2}.}
7723:. The four common points are called the
7154:and two tangents (the vertical lines at
6855:
6139:
5211:
5114:
4832:
3454:, which is a special case of an ellipse;
1798:
1790:
1782:
635:
380:
251:
102:'s systematic work on their properties.
45:
37:
29:
10396:College Calculus with Analytic Geometry
10338:The Mathematical Association of America
10240:, Springer Science & Business Media
10235:
10212:
10126:Akopyan, A.V.; Zaslavsky, A.A. (2007).
9882:
9870:
9790:
9587:
9401:The Thirteen Books of Euclid's Elements
9168:, John Wiley and Sons, pp. 44–45,
7742:matrix representation of conic sections
6988:(the lengths of these segments will be
6091:and the absolute line, with respect to
5424:a conic section can be represented as:
2879:Matrix representation of conic sections
1779:Standard forms in Cartesian coordinates
14:
11141:
10966:Clifford's theorem on special divisors
10432:
10331:
9467:
9316:"A gallery of conics by five elements"
9161:
9065:
7117:will be points of the ellipse between
6621:. Thus, a polarity associates a point
5110:
4000:{\displaystyle \Delta e^{4}+e^{2}-=0,}
27:Curve from a cone intersecting a plane
10524:
10496:
10244:
10169:
10148:
10096:(Berlin/Heidelberg: Springer, 2010),
9933:
9921:
9909:
9739:
9727:
9703:
9688:
9455:
9375:
9363:
9351:
9225:
8950:
8856:as hyperbolic. This is elaborated at
8269:where the number of +1 coefficients,
7136:with the lines of the pencil through
6130:Steiner's projective conic definition
5968:
5327:Newton's law of universal gravitation
5123:, in a 9th-century Arabic translation
3602:Eccentricity in terms of coefficients
2761:
1674:{\displaystyle {\sqrt {a^{2}+b^{2}}}}
1280:{\displaystyle {\sqrt {a^{2}-b^{2}}}}
326:There are three types of conics: the
317:
247:
119:, and some particular line, called a
10306:
10285:
10264:
9842:
9802:
9778:
9676:
9443:
9412:
9387:
9000:
7860:identify the homogeneous parameters
7377:. If the points at infinity are the
7010:times the length of the segments on
6611:between the points and the lines of
5261:both applied their newly discovered
5004:lines that are tangent to it, for 0≤
4828:
4779:
3865:
3579:
2362:These standard forms can be written
871:{\displaystyle \ p+c={\frac {a}{e}}}
264:
10480:Wilson, W.A.; Tracey, J.I. (1925),
7740:solutions exploits the homogeneous
7700:
7409:
5329:are conic sections if their common
3598:are invariant under rotation only.
1014:{\displaystyle x^{2}+y^{2}=a^{2}\,}
631:
123:, are in a fixed ratio, called the
24:
11124:Vector bundles on algebraic curves
11058:Weber's theorem (Algebraic curves)
10655:Hasse's theorem on elliptic curves
10645:Counting points on elliptic curves
10446:Undergraduate Texts in Mathematics
9291:
8842:discrete probability distributions
8595:is a more complicated object, but
8059:
7311:Further unification occurs in the
6002:as points in the five-dimensional
4789:
4498:
4440:
4017:
3982:
3932:
3885:
2872:
2033:{\displaystyle x^{2}+y^{2}=a^{2},}
1819:) these equations can be put into
1709:{\displaystyle {\frac {b^{2}}{a}}}
1315:{\displaystyle {\frac {b^{2}}{a}}}
1095:
25:
11180:
10489:
10270:A Survey of Geometry (Volume One)
10046:A Catalog of Special Plane Curves
7748:which depends on six parameters.
7690:, or two intersecting lines when
7577:point is the intersection of two
6980:, to form equal segments on side
6731:Specifically, given five points,
6040:Projective definition of a circle
6030:{\displaystyle \mathbf {P} ^{5}.}
3872:if that determinant is positive.
644:In addition to the eccentricity (
377:Eccentricity, focus and directrix
10377:Fundamental Concepts of Geometry
8474:(flat, parabola), or negative –
8444:(all positive or all negative),
8134:variables can be converted to a
8117:Quadratic form classifications:
7542:{\displaystyle x^{2}+y^{2}+1=0.}
7337:), so there are between 1 and 4
7322:projective linear transformation
6908:, first construct the rectangle
6719:
6087:of the point of intersection of
6014:
5317:Conic sections are important in
5272:Tractatus de sectionibus conicis
5169:
4855:-axis, is given by the equation
434:whose distance to a fixed point
10746:Hurwitz's automorphisms theorem
10414:Richter-Gebert, Jürgen (2011).
10119:
10103:
10083:
10067:
10035:
10021:
9992:
9987:Brannan, Esplen & Gray 1999
9980:
9973:10.1090/s0002-9904-1916-02785-6
9951:
9939:
9927:
9915:
9903:
9888:
9876:
9864:
9848:
9836:
9831:(German) Part II follows Part I
9820:
9808:
9784:
9772:
9757:
9745:
9733:
9721:
9716:Brannan, Esplen & Gray 1999
9709:
9682:
9670:
9638:
9606:
9581:
9556:
9524:
9492:
9461:
9449:
9437:
9418:
9406:
9393:
9381:
9369:
9357:
9345:
9340:Brannan, Esplen & Gray 1999
9333:
9307:
9286:Brannan, Esplen & Gray 1999
9279:
9264:
9258:The College Mathematics Journal
9249:
9212:
9200:
9155:
9150:Brannan, Esplen & Gray 1999
9143:
9131:
9119:
9090:Brannan, Esplen & Gray 1999
9078:Brannan, Esplen & Gray 1999
9062:Brannan, Esplen & Gray 1999
9013:Brannan, Esplen & Gray 1999
8974:
8965:
8956:
8939:
8930:
8854:negative binomial distributions
7885:{\displaystyle (\lambda ,\mu )}
7420:What should be considered as a
7169:In the complex projective plane
6577:Karl Georg Christian von Staudt
5742:the matrix of the conic section
5293:
5026:All the conic sections share a
3274:
1875:for a hyperbola. For a circle,
308:, with the surface of a double
10971:Gonality of an algebraic curve
10882:Differential of the first kind
10464:Calculus and Analytic Geometry
10199:, Cambridge University Press,
10029:"MathWorld: Cylindric section"
9107:
9095:
9083:
9071:
9055:
9043:
9018:
9006:
8994:
8801:
8790:
8751:
8740:
8702:
8691:
8610:Partial differential equations
7934:
7902:
7879:
7867:
7715:in general position (no three
7086:. The points of intersection,
6849:. By varying the line through
6533:
6429:
6423:
6400:
6394:
6343:
6337:
6314:
6308:
6191:
6185:
6176:
6170:
4780:3 × 3 matrix above
4736:
4727:
4712:
4700:
4691:
4679:
4501:
4485:
4461:
4443:
4427:
4403:
4356:
4328:
4304:
4286:
4258:
4234:
4199:
4184:
3985:
3967:
3954:
3951:
3935:
3917:
3904:
3901:
3866:3 × 3 matrix above
3816:
3803:
3795:
3783:
3754:
3741:
3580:3 × 3 matrix above
2640:
2607:
2596:
2566:
2534:
2506:
2474:
2444:
2412:
2382:
767:The following relations hold:
133:, a conic may be defined as a
13:
1:
11114:Birkhoff–Grothendieck theorem
10824:Nagata's conjecture on curves
10695:Schoof–Elkies–Atkin algorithm
10569:Five points determine a conic
10132:American Mathematical Society
8987:
8105:In other areas of mathematics
7296:{\displaystyle x^{2}-w^{2}=1}
7218:{\displaystyle x^{2}+y^{2}=1}
6085:projective harmonic conjugate
5156:
5132:
5093:
4975:five points determine a conic
4968:
4944:the graph is an ellipse, for
4936:, the graph is a circle, for
4072:Ellipse § Canonical form
3535:
3426:, the equation represents an
2543:{\displaystyle (at^{2},2at),}
1803:Standard forms of a hyperbola
410:). The conic of eccentricity
295:
10685:Supersingular elliptic curve
10374:Merserve, Bruce E. (1983) ,
10176:History of Analytic Geometry
10042:Lawrence, J. Dennis (1972),
9946:Akopyan & Zaslavsky 2007
9403:, Vol. I, Dover, 1956, pg.16
9222:, Dover Publ., 1966, p. 110.
9220:Matrices and Transformations
8634:Eccentricity classifications
8514:{\displaystyle x^{2}+y^{2},}
8315:{\displaystyle k+\ell +m=n.}
7497:, such as with the equation
5404:other non-degenerate conic.
5353:In the real projective plane
4576:{\displaystyle \lambda _{2}}
4549:{\displaystyle \lambda _{1}}
4066:Conversion to canonical form
3506:, the equation represents a
3488:, the equation represents a
3470:, the equation represents a
3450:, the equation represents a
1795:Standard forms of a parabola
1787:Standard forms of an ellipse
659:. A parabola has no center.
96:ancient Greek mathematicians
7:
10892:Riemann's existence theorem
10819:Hilbert's sixteenth problem
10711:Elliptic curve cryptography
10624:Fundamental pair of periods
9618:Mathematics and its history
9515:John Wiley & Sons, Inc.
9261:34(2), March 2003, 116–121.
9104:, pp. 314–328, 585–589
8876:
8580:{\displaystyle x^{2}-y^{2}}
8428:{\displaystyle x^{2}-y^{2}}
8357:{\displaystyle x^{2}+y^{2}}
7996:given the degenerate conic
7744:, i.e. a 3 × 3
6753:and a line passing through
6108:circular points at infinity
3516:In the notation used here,
2750:Cartesian coordinate system
1420:{\displaystyle y^{2}=4ax\,}
10:
11185:
11022:Moduli of algebraic curves
9468:Turner, Howard R. (1997).
9427:Treatise on Conic Sections
8898:Elliptic coordinate system
8128:Sylvester's law of inertia
7704:
7486:{\displaystyle x^{2}+1=0,}
7413:
7060:label the upper endpoints
6569:
6133:
5347:Herschel optical telescope
5297:
5282:Elementa Curvarum Linearum
5101:Quadrature of the Parabola
5066:Menaechmus and early works
5060:
4926:is the semi-latus rectum.
4778:is the determinant of the
4069:
3864:if the determinant of the
2876:
795:{\displaystyle \ \ell =pe}
474:we obtain an ellipse, for
403:), and a hyperbola (blue,
385:Conic sections of varying
105:The conic sections in the
11104:
11066:
11035:
10999:
10948:
10941:
10915:
10847:
10764:
10728:
10703:
10637:
10606:
10597:
10559:
10398:(2nd ed.), Reading:
10272:, Boston: Allyn and Bacon
10238:The Real Projective Plane
9476:University of Texas Press
9195:Protter & Morrey 1970
9138:Protter & Morrey 1970
9114:Protter & Morrey 1970
9102:Protter & Morrey 1970
7396:, the conic section is a
7327:It can be proven that in
6197:{\displaystyle B(U),B(V)}
5207:
5119:Diagram from Apollonius'
3311:{\displaystyle B^{2}-4AC}
2309:{\displaystyle xy=c^{2}.}
444:) is a constant multiple
11154:Euclidean solid geometry
10789:Cayley–Bacharach theorem
10716:Elliptic curve primality
10354:Faulkner, T. E. (1952),
10236:Coxeter, H.S.M. (1993),
9507:A History of Mathematics
9314:Pamfilos, Paris (2014).
9298:Whitworth, William Allen
9207:Wilson & Tracey 1925
9162:Fanchi, John R. (2006),
9126:Wilson & Tracey 1925
9050:Thomas & Finney 1979
8923:
8593:Riemann curvature tensor
7966:{\displaystyle \lambda }
7313:complex projective plane
6598:, of a projective plane
6079:is defined as the point
5395:Intersection at infinity
5138:BC), whose eight-volume
5105:On Conoids and Spheroids
4920:is the eccentricity and
906:{\displaystyle a,b>0}
591:focus-directrix property
534:{\displaystyle \alpha ,}
256:Types of conic sections:
11048:Riemann–Hurwitz formula
11012:Gromov–Witten invariant
10872:Compact Riemann surface
10660:Mazur's torsion theorem
8888:Circumconic and inconic
8883:Confocal conic sections
8093:The intersection of an
8076:require division by 2.
7735:Intersecting two conics
7579:complex conjugate lines
6566:Von Staudt's definition
6204:of lines at two points
5422:homogeneous coordinates
5416:Homogeneous coordinates
5387:(and its corresponding
5364:homogeneous coordinates
5231:principle of continuity
4979:general linear position
2275:Rectangular hyperbola:
1101:{\displaystyle \infty }
454:) of the distance from
358:: the plane intersects
10665:Modular elliptic curve
10332:Kendig, Keith (2005),
9960:Bull. Amer. Math. Soc.
9531:Van der Waerden, B. L.
9218:Pettofrezzo, Anthony,
8873:
8846:binomial distributions
8836:Variance-to-mean ratio
8826:
8776:
8727:
8641:Möbius transformations
8625:is parabolic, and the
8589:uniformization theorem
8581:
8541:
8515:
8429:
8387:
8358:
8316:
8263:
8047:
8017:
7987:
7967:
7947:
7886:
7852:
7803:
7776:
7543:
7487:
7297:
7251:
7219:
6865:ellipse with equation
6861:
6845:at the required point
6524:
6484:
6466:, which is called the
6460:
6436:
6407:
6378:
6350:
6321:
6292:
6264:
6244:
6230:(all lines containing
6224:
6198:
6145:
6031:
5955:
5860:
5731:
5525:
5281:
5271:
5223:
5186:using conic sections.
5176:Islamic mathematicians
5124:
4905:
4842:
4819:
4772:
4749:
4650:
4577:
4550:
4520:
4375:
4209:
4162:
4056:
4001:
3851:
3695:
3399:
3312:
3259:
3061:
2861:with all coefficients
2852:
2744:General Cartesian form
2732:
2647:
2544:
2484:
2422:
2310:
2265:
2182:
2117:
2034:
1804:
1796:
1788:
1767:
1710:
1675:
1630:
1578:
1496:
1471:
1443:
1421:
1373:
1316:
1281:
1236:
1184:
1102:
1081:
1059:
1037:
1015:
907:
872:
829:
828:{\displaystyle \ c=ae}
796:
641:
581:
535:
512:
511:{\displaystyle \beta }
423:
396:), a parabola (green,
285:
223:
51:
43:
35:
10579:Rational normal curve
10245:Downs, J.W. (2003) ,
9424:Apollonius of Perga,
9276:66(5), 1993, 322–325.
8908:Parabolic coordinates
8867:
8850:Poisson distributions
8827:
8777:
8728:
8659:or its 2-fold cover,
8582:
8542:
8540:{\displaystyle x^{2}}
8516:
8430:
8388:
8386:{\displaystyle x^{2}}
8359:
8317:
8264:
8048:
8046:{\displaystyle C_{0}}
8018:
8016:{\displaystyle C_{0}}
7988:
7968:
7948:
7887:
7853:
7804:
7802:{\displaystyle C_{2}}
7777:
7775:{\displaystyle C_{1}}
7755:given the two conics
7676:we have a point when
7544:
7488:
7414:Further information:
7298:
7252:
7250:{\displaystyle y=iw,}
7220:
7173:In the complex plane
6859:
6525:
6485:
6470:of the perspectivity
6461:
6437:
6408:
6379:
6351:
6322:
6293:
6265:
6245:
6225:
6199:
6143:
6032:
5956:
5861:
5732:
5526:
5360:real projective plane
5285:starts with Kepler's
5269:in his 1655 treatise
5215:
5193:used conics to solve
5118:
4906:
4836:
4820:
4773:
4750:
4651:
4578:
4551:
4521:
4376:
4210:
4163:
4057:
4002:
3852:
3696:
3508:rectangular hyperbola
3400:
3313:
3260:
3062:
2853:
2733:
2659:Rectangular hyperbola
2648:
2545:
2485:
2423:
2311:
2266:
2183:
2118:
2035:
1809:Cartesian coordinates
1802:
1794:
1786:
1768:
1711:
1676:
1631:
1579:
1497:
1472:
1444:
1422:
1374:
1317:
1282:
1237:
1185:
1103:
1082:
1060:
1038:
1016:
934:linear eccentricity (
908:
873:
830:
797:
639:
582:
536:
513:
414:in this figure is an
384:
255:
240:coordinates to admit
224:
135:plane algebraic curve
49:
41:
33:
11119:Stable vector bundle
10991:Weil reciprocity law
10981:Riemann–Roch theorem
10961:Brill–Noether theory
10897:Riemann–Roch theorem
10814:Genus–degree formula
10675:Mordell–Weil theorem
10650:Division polynomials
9273:Mathematics Magazine
9181:Section 3.2, page 45
8953:, p.14, footnote 14.
8870:this interactive SVG
8786:
8736:
8681:
8551:
8524:
8482:
8399:
8370:
8328:
8285:
8142:
8030:
8000:
7986:{\displaystyle \mu }
7977:
7957:
7896:
7864:
7813:
7786:
7759:
7501:
7455:
7261:
7229:
7183:
6540:Principle of Duality
6508:
6483:{\displaystyle \pi }
6474:
6450:
6435:{\displaystyle B(V)}
6417:
6406:{\displaystyle B(U)}
6388:
6377:{\displaystyle \pi }
6368:
6349:{\displaystyle B(V)}
6331:
6320:{\displaystyle B(U)}
6302:
6291:{\displaystyle \pi }
6282:
6254:
6234:
6208:
6164:
6009:
5876:
5754:
5545:
5431:
5377:The Euclidean plane
5343:parabolic microphone
5249:hexagrammum mysticum
5153:Pappus of Alexandria
5076:Duplicating the cube
4951:a parabola, and for
4862:
4786:
4762:
4663:
4591:
4560:
4533:
4391:
4222:
4175:
4083:
4014:
3882:
3723:
3613:
3582:. The constant term
3337:
3283:
3073:
2887:
2771:
2667:
2563:
2503:
2441:
2379:
2281:
2198:
2133:
2050:
1988:
1721:
1686:
1641:
1589:
1514:
1495:{\displaystyle 2a\,}
1482:
1470:{\displaystyle 2a\,}
1457:
1432:
1391:
1327:
1292:
1247:
1195:
1120:
1092:
1070:
1048:
1026:
971:
885:
840:
807:
774:
545:
541:the eccentricity is
522:
502:
481:a parabola, and for
145:
11164:Birational geometry
10942:Structure of curves
10834:Quartic plane curve
10756:Hyperelliptic curve
10736:De Franchis theorem
10680:Nagell–Lutz theorem
10440:Projective Geometry
10357:Projective Geometry
10303:(PDF; 891 kB).
10219:Projective Geometry
10110:Richter-Gebert 2011
9998:Korn, G. A., &
9730:, p. 158, Thm 3-5.1
9323:Forum Geometricorum
9034:Thomson Brooks/Cole
8601:sectional curvature
8476:hyperbolic geometry
8255:
8225:
8201:
8177:
8159:
8097:with a sphere is a
6617:that preserves the
6523:{\displaystyle U,V}
6223:{\displaystyle U,V}
5245:projective geometry
5129:Apollonius of Perga
5111:Apollonius of Perga
5028:reflection property
4981:, meaning no three
4355:
4275:
1915:-axis at the point
1861:for an ellipse and
1817:translation of axes
1442:{\displaystyle 1\,}
1080:{\displaystyle a\,}
1058:{\displaystyle 0\,}
1036:{\displaystyle 0\,}
943:semi-latus rectum (
664:linear eccentricity
100:Apollonius of Perga
10949:Divisors on curves
10741:Faltings's theorem
10690:Schoof's algorithm
10670:Modularity theorem
10498:Weisstein, Eric W.
10281:, Berlin: Springer
10128:Geometry of Conics
10012:Dover Publications
9116:, pp. 290–314
9068:, pp. 86, 141
8913:Quadratic function
8874:
8852:as parabolic, and
8822:
8772:
8723:
8577:
8537:
8511:
8472:Euclidean geometry
8460:Gaussian curvature
8425:
8383:
8354:
8312:
8259:
8235:
8205:
8187:
8163:
8145:
8088:generalized conics
8066:pappian geometries
8043:
8013:
7983:
7963:
7943:
7882:
7848:
7799:
7772:
7571:cylindric sections
7557:line (a line with
7539:
7483:
7357:Furthermore, each
7293:
7247:
7215:
7082:and going towards
7048:and going towards
6960:. Divide the side
6862:
6619:incidence relation
6585:Geometrie der Lage
6520:
6480:
6456:
6432:
6403:
6374:
6346:
6317:
6288:
6260:
6240:
6220:
6194:
6160:Given two pencils
6146:
6027:
5951:
5942:
5856:
5727:
5715:
5682:
5571:
5521:
5389:points at infinity
5224:
5125:
5023:(or outer point).
4987:further discussion
4901:
4843:
4815:
4768:
4745:
4646:
4640:
4573:
4546:
4516:
4371:
4341:
4261:
4205:
4158:
4052:
3997:
3847:
3691:
3395:
3386:
3332:matrix determinant
3308:
3255:
3243:
3210:
3099:
3057:
3039:
3013:
2986:
2960:
2908:
2848:
2758:quadratic equation
2728:
2643:
2540:
2480:
2418:
2306:
2261:
2178:
2113:
2030:
1807:After introducing
1805:
1797:
1789:
1763:
1706:
1671:
1626:
1574:
1492:
1467:
1439:
1417:
1369:
1312:
1277:
1232:
1180:
1098:
1077:
1055:
1033:
1011:
903:
868:
825:
792:
756:), the same value
642:
577:
531:
508:
424:
290:Euclidean geometry
286:
248:Euclidean geometry
219:
139:quadratic equation
52:
44:
36:
11169:Analytic geometry
11136:
11135:
11132:
11131:
11043:Hasse–Witt matrix
10986:Weierstrass point
10933:Smooth completion
10902:Teichmüller space
10804:Cubic plane curve
10724:
10723:
10638:Arithmetic theory
10619:Elliptic integral
10614:Elliptic function
10482:Analytic Geometry
10347:978-0-88385-335-1
10325:978-0-321-01618-8
10286:Hartmann, Erich,
10206:978-0-521-59787-6
10186:978-0-486-43832-0
10163:978-0-486-46627-9
10141:978-0-8218-4323-9
10050:, Dover, p.
9833:) Part II, pg. 96
9631:978-1-4419-6052-8
9599:978-3-642-51599-6
9574:978-3-642-36736-6
9239:Analytical Conics
8621:is elliptic, the
8606:Second order PDEs
8587:. Indeed, by the
8468:elliptic geometry
8448:(some zeros), or
7729:pencil of circles
7495:imaginary ellipse
7449:complex conjugate
7402:complex conjugate
6554:(or dual conic).
6459:{\displaystyle a}
6263:{\displaystyle V}
6243:{\displaystyle U}
6050:projective planes
5263:analytic geometry
5216:Table of conics,
4896:
4847:polar coordinates
4829:Polar coordinates
4771:{\displaystyle S}
4505:
4464:
4447:
4406:
4360:
4307:
4290:
4237:
4202:
4187:
4047:
3842:
3841:
3838:
3776:
3540:The discriminant
2723:
2722:
2705:
2704: where
2692:
2605:
2250:
2223:
2164:
2102:
2075:
1847:by the equations
1776:
1775:
1761:
1760:
1704:
1669:
1624:
1622:
1566:
1539:
1367:
1366:
1310:
1275:
1230:
1228:
1172:
1145:
952:focal parameter (
866:
845:
812:
779:
683:semi-latus rectum
572:
312:(a cone with two
131:analytic geometry
16:(Redirected from
11176:
11159:Algebraic curves
10976:Jacobian variety
10946:
10945:
10849:Riemann surfaces
10839:Real plane curve
10799:Cramer's paradox
10779:Bézout's theorem
10604:
10603:
10553:algebraic curves
10545:
10538:
10531:
10522:
10521:
10511:
10510:
10485:
10476:
10458:
10443:
10429:
10410:
10390:
10370:
10350:
10328:
10317:
10302:
10301:
10299:
10294:
10282:
10273:
10261:
10241:
10232:
10209:
10189:
10166:
10145:
10113:
10107:
10101:
10087:
10081:
10071:
10065:
10064:
10049:
10039:
10033:
10032:
10025:
10019:
9996:
9990:
9984:
9978:
9976:
9975:
9955:
9949:
9943:
9937:
9931:
9925:
9919:
9913:
9907:
9901:
9892:
9886:
9880:
9874:
9868:
9862:
9852:
9846:
9840:
9834:
9824:
9818:
9812:
9806:
9800:
9794:
9788:
9782:
9776:
9770:
9761:
9755:
9749:
9743:
9737:
9731:
9725:
9719:
9713:
9707:
9701:
9692:
9686:
9680:
9674:
9668:
9667:
9665:
9663:
9657:
9651:. Archived from
9650:
9642:
9636:
9635:
9610:
9604:
9603:
9585:
9579:
9578:
9560:
9554:
9528:
9522:
9496:
9490:
9489:
9465:
9459:
9453:
9447:
9441:
9435:
9422:
9416:
9410:
9404:
9397:
9391:
9385:
9379:
9373:
9367:
9366:, pp. 17–18
9361:
9355:
9354:, pp. 36ff.
9349:
9343:
9337:
9331:
9330:
9320:
9311:
9305:
9295:
9289:
9283:
9277:
9268:
9262:
9253:
9247:
9234:
9223:
9216:
9210:
9204:
9198:
9192:
9183:
9178:
9159:
9153:
9147:
9141:
9135:
9129:
9123:
9117:
9111:
9105:
9099:
9093:
9092:, pp. 11–16
9087:
9081:
9080:, pp. 13–16
9075:
9069:
9059:
9053:
9047:
9041:
9022:
9016:
9010:
9004:
8998:
8981:
8978:
8972:
8969:
8963:
8960:
8954:
8943:
8937:
8934:
8831:
8829:
8828:
8823:
8809:
8804:
8793:
8781:
8779:
8778:
8773:
8759:
8754:
8743:
8732:
8730:
8729:
8724:
8710:
8705:
8694:
8671:
8657:
8619:Poisson equation
8586:
8584:
8583:
8578:
8576:
8575:
8563:
8562:
8546:
8544:
8543:
8538:
8536:
8535:
8520:
8518:
8517:
8512:
8507:
8506:
8494:
8493:
8434:
8432:
8431:
8426:
8424:
8423:
8411:
8410:
8392:
8390:
8389:
8384:
8382:
8381:
8363:
8361:
8360:
8355:
8353:
8352:
8340:
8339:
8321:
8319:
8318:
8313:
8268:
8266:
8265:
8260:
8254:
8249:
8224:
8219:
8200:
8195:
8176:
8171:
8158:
8153:
8052:
8050:
8049:
8044:
8042:
8041:
8022:
8020:
8019:
8014:
8012:
8011:
7992:
7990:
7989:
7984:
7972:
7970:
7969:
7964:
7953:and solving for
7952:
7950:
7949:
7944:
7933:
7932:
7917:
7916:
7891:
7889:
7888:
7883:
7857:
7855:
7854:
7849:
7844:
7843:
7828:
7827:
7808:
7806:
7805:
7800:
7798:
7797:
7781:
7779:
7778:
7773:
7771:
7770:
7746:symmetric matrix
7721:pencil of conics
7701:Pencil of conics
7696:
7689:
7682:
7675:
7668:
7661:
7647:
7646:
7644:
7643:
7640:
7637:
7616:
7614:
7613:
7610:
7607:
7589:
7548:
7546:
7545:
7540:
7526:
7525:
7513:
7512:
7492:
7490:
7489:
7484:
7467:
7466:
7416:Degenerate conic
7410:Degenerate cases
7395:
7387:
7332:
7319:
7305:line at infinity
7302:
7300:
7299:
7294:
7286:
7285:
7273:
7272:
7256:
7254:
7253:
7248:
7224:
7222:
7221:
7216:
7208:
7207:
7195:
7194:
7178:
7161:
7157:
7153:
7149:
7139:
7135:
7131:
7120:
7116:
7105:
7101:
7092:
7085:
7081:
7077:
7068:
7059:
7058:
7051:
7047:
7043:
7034:
7025:
7024:
7017:
7016:
7009:
7008:
7006:
7005:
7000:
6997:
6987:
6986:
6979:
6978:
6971:
6967:
6966:
6959:
6948:
6913:
6907:
6905:
6903:
6902:
6897:
6894:
6885:
6883:
6882:
6877:
6874:
6852:
6848:
6844:
6843:
6836:
6835:
6828:
6824:
6823:
6816:
6815:
6808:
6804:
6803:
6796:
6795:
6788:
6784:
6783:
6776:
6775:
6768:
6764:
6763:
6756:
6752:
6700:
6688:
6682:
6670:
6660:
6646:
6632:
6626:
6616:
6603:
6597:
6572:Von Staudt conic
6560:point of contact
6529:
6527:
6526:
6521:
6489:
6487:
6486:
6481:
6465:
6463:
6462:
6457:
6441:
6439:
6438:
6433:
6412:
6410:
6409:
6404:
6383:
6381:
6380:
6375:
6355:
6353:
6352:
6347:
6326:
6324:
6323:
6318:
6297:
6295:
6294:
6289:
6269:
6267:
6266:
6261:
6249:
6247:
6246:
6241:
6229:
6227:
6226:
6221:
6203:
6201:
6200:
6195:
6124:
6098:
6094:
6090:
6082:
6078:
6075:of line segment
6070:
6066:
6036:
6034:
6033:
6028:
6023:
6022:
6017:
6004:projective space
6001:
5960:
5958:
5957:
5952:
5947:
5943:
5865:
5863:
5862:
5857:
5846:
5845:
5800:
5799:
5769:
5768:
5736:
5734:
5733:
5728:
5720:
5716:
5687:
5683:
5671:
5658:
5643:
5625:
5610:
5597:
5576:
5572:
5530:
5528:
5527:
5522:
5514:
5513:
5474:
5473:
5446:
5445:
5401:projective space
5385:line at infinity
5382:
5345:. The 4.2 meter
5335:two-body problem
5284:
5274:
5237:Girard Desargues
5161:
5158:
5137:
5134:
5098:
5095:
5040:Pappus's theorem
5035:Pascal's theorem
4957:
4950:
4943:
4935:
4925:
4919:
4910:
4908:
4907:
4902:
4897:
4895:
4872:
4854:
4824:
4822:
4821:
4816:
4814:
4813:
4804:
4803:
4777:
4775:
4774:
4769:
4754:
4752:
4751:
4746:
4735:
4734:
4722:
4675:
4674:
4655:
4653:
4652:
4647:
4645:
4641:
4629:
4614:
4582:
4580:
4579:
4574:
4572:
4571:
4555:
4553:
4552:
4547:
4545:
4544:
4525:
4523:
4522:
4517:
4506:
4504:
4497:
4496:
4484:
4472:
4471:
4466:
4465:
4457:
4453:
4448:
4446:
4439:
4438:
4426:
4414:
4413:
4408:
4407:
4399:
4395:
4384:or equivalently
4380:
4378:
4377:
4372:
4361:
4359:
4354:
4349:
4340:
4339:
4327:
4315:
4314:
4309:
4308:
4300:
4296:
4291:
4289:
4285:
4284:
4274:
4269:
4257:
4245:
4244:
4239:
4238:
4230:
4226:
4214:
4212:
4211:
4206:
4204:
4203:
4195:
4189:
4188:
4180:
4167:
4165:
4164:
4159:
4126:
4125:
4098:
4097:
4061:
4059:
4058:
4053:
4048:
4043:
4042:
4033:
4006:
4004:
4003:
3998:
3975:
3974:
3947:
3946:
3925:
3924:
3897:
3896:
3871:
3868:is negative and
3863:
3856:
3854:
3853:
3848:
3843:
3840:
3839:
3837:
3836:
3824:
3823:
3802:
3778:
3777:
3775:
3774:
3762:
3761:
3740:
3734:
3733:
3714:
3700:
3698:
3697:
3692:
3656:
3655:
3628:
3627:
3597:
3587:
3573:
3563:
3549:
3531:
3527:
3523:
3519:
3505:
3487:
3469:
3449:
3442:
3425:
3407:If the conic is
3404:
3402:
3401:
3396:
3391:
3387:
3375:
3360:
3329:
3325:
3317:
3315:
3314:
3309:
3295:
3294:
3264:
3262:
3261:
3256:
3248:
3247:
3215:
3214:
3199:
3186:
3171:
3153:
3138:
3125:
3104:
3103:
3066:
3064:
3063:
3058:
3044:
3043:
3018:
3017:
2991:
2990:
2965:
2964:
2949:
2934:
2913:
2912:
2868:
2857:
2855:
2854:
2849:
2814:
2813:
2786:
2785:
2737:
2735:
2734:
2729:
2724:
2718:
2714:
2706:
2703:
2698:
2694:
2693:
2685:
2652:
2650:
2649:
2644:
2606:
2603:
2549:
2547:
2546:
2541:
2521:
2520:
2489:
2487:
2486:
2481:
2427:
2425:
2424:
2419:
2358:
2348:
2338:
2332:
2326:
2315:
2313:
2312:
2307:
2302:
2301:
2270:
2268:
2267:
2262:
2251:
2249:
2248:
2239:
2238:
2229:
2224:
2222:
2221:
2212:
2211:
2202:
2187:
2185:
2184:
2179:
2165:
2163: with
2162:
2145:
2144:
2122:
2120:
2119:
2114:
2103:
2101:
2100:
2091:
2090:
2081:
2076:
2074:
2073:
2064:
2063:
2054:
2039:
2037:
2036:
2031:
2026:
2025:
2013:
2012:
2000:
1999:
1977:
1965:
1953:
1932:
1922:
1914:
1910:
1891:
1881:
1874:
1860:
1846:
1842:
1834:
1826:
1772:
1770:
1769:
1764:
1762:
1759:
1758:
1746:
1745:
1736:
1735:
1734:
1725:
1715:
1713:
1712:
1707:
1705:
1700:
1699:
1690:
1680:
1678:
1677:
1672:
1670:
1668:
1667:
1655:
1654:
1645:
1635:
1633:
1632:
1627:
1625:
1623:
1621:
1620:
1611:
1610:
1601:
1593:
1583:
1581:
1580:
1575:
1567:
1565:
1564:
1555:
1554:
1545:
1540:
1538:
1537:
1528:
1527:
1518:
1501:
1499:
1498:
1493:
1476:
1474:
1473:
1468:
1448:
1446:
1445:
1440:
1426:
1424:
1423:
1418:
1403:
1402:
1378:
1376:
1375:
1370:
1368:
1365:
1364:
1352:
1351:
1342:
1341:
1340:
1331:
1321:
1319:
1318:
1313:
1311:
1306:
1305:
1296:
1286:
1284:
1283:
1278:
1276:
1274:
1273:
1261:
1260:
1251:
1241:
1239:
1238:
1233:
1231:
1229:
1227:
1226:
1217:
1216:
1207:
1199:
1189:
1187:
1186:
1181:
1173:
1171:
1170:
1161:
1160:
1151:
1146:
1144:
1143:
1134:
1133:
1124:
1107:
1105:
1104:
1099:
1086:
1084:
1083:
1078:
1064:
1062:
1061:
1056:
1042:
1040:
1039:
1034:
1020:
1018:
1017:
1012:
1009:
1008:
996:
995:
983:
982:
957:
948:
939:
930:
916:
915:
912:
910:
909:
904:
877:
875:
874:
869:
867:
859:
843:
834:
832:
831:
826:
810:
801:
799:
798:
793:
777:
763:
759:
755:
740:
736:
728:
720:
716:
699:
688:
669:
647:
632:Conic parameters
627:
619:
613:
606:
595:Dandelin spheres
586:
584:
583:
578:
573:
571:
560:
549:
540:
538:
537:
532:
517:
515:
514:
509:
487:
480:
473:
461:
458:to a fixed line
457:
447:
437:
433:
421:
413:
409:
402:
395:
284:
277:
270:
263:
234:projective plane
228:
226:
225:
220:
188:
187:
160:
159:
70:obtained from a
21:
11184:
11183:
11179:
11178:
11177:
11175:
11174:
11173:
11139:
11138:
11137:
11128:
11100:
11091:Delta invariant
11062:
11031:
10995:
10956:Abel–Jacobi map
10937:
10911:
10907:Torelli theorem
10877:Dessin d'enfant
10857:Belyi's theorem
10843:
10829:Plücker formula
10760:
10751:Hurwitz surface
10720:
10699:
10633:
10607:Analytic theory
10599:Elliptic curves
10593:
10574:Projective line
10561:Rational curves
10555:
10549:
10501:"Conic Section"
10492:
10474:
10456:
10426:
10388:
10368:
10348:
10326:
10308:Katz, Victor J.
10297:
10295:
10292:
10259:
10230:
10214:Coxeter, H.S.M.
10207:
10187:
10164:
10154:Linear Geometry
10142:
10122:
10117:
10116:
10108:
10104:
10088:
10084:
10072:
10068:
10062:
10040:
10036:
10027:
10026:
10022:
9997:
9993:
9985:
9981:
9956:
9952:
9944:
9940:
9932:
9928:
9920:
9916:
9908:
9904:
9893:
9889:
9881:
9877:
9869:
9865:
9853:
9849:
9841:
9837:
9825:
9821:
9813:
9809:
9801:
9797:
9789:
9785:
9777:
9773:
9762:
9758:
9750:
9746:
9738:
9734:
9726:
9722:
9714:
9710:
9702:
9695:
9687:
9683:
9675:
9671:
9661:
9659:
9655:
9648:
9644:
9643:
9639:
9632:
9614:Stillwell, John
9611:
9607:
9600:
9586:
9582:
9575:
9561:
9557:
9547:Springer Verlag
9529:
9525:
9503:Merzbach, U. C.
9497:
9493:
9486:
9466:
9462:
9454:
9450:
9442:
9438:
9423:
9419:
9411:
9407:
9398:
9394:
9386:
9382:
9374:
9370:
9362:
9358:
9350:
9346:
9338:
9334:
9318:
9312:
9308:
9296:
9292:
9284:
9280:
9269:
9265:
9254:
9250:
9235:
9226:
9217:
9213:
9205:
9201:
9193:
9186:
9176:
9160:
9156:
9148:
9144:
9136:
9132:
9124:
9120:
9112:
9108:
9100:
9096:
9088:
9084:
9076:
9072:
9060:
9056:
9048:
9044:
9023:
9019:
9011:
9007:
8999:
8995:
8990:
8985:
8984:
8979:
8975:
8970:
8966:
8961:
8957:
8944:
8940:
8935:
8931:
8926:
8918:Spherical conic
8903:Equidistant set
8893:Director circle
8879:
8848:as elliptical,
8805:
8800:
8789:
8787:
8784:
8783:
8755:
8750:
8739:
8737:
8734:
8733:
8706:
8701:
8690:
8682:
8679:
8678:
8665:
8661:
8651:
8647:
8571:
8567:
8558:
8554:
8552:
8549:
8548:
8531:
8527:
8525:
8522:
8521:
8502:
8498:
8489:
8485:
8483:
8480:
8479:
8419:
8415:
8406:
8402:
8400:
8397:
8396:
8377:
8373:
8371:
8368:
8367:
8348:
8344:
8335:
8331:
8329:
8326:
8325:
8286:
8283:
8282:
8250:
8239:
8220:
8209:
8196:
8191:
8172:
8167:
8154:
8149:
8143:
8140:
8139:
8122:Quadratic forms
8107:
8099:spherical conic
8062:
8060:Generalizations
8037:
8033:
8031:
8028:
8027:
8007:
8003:
8001:
7998:
7997:
7978:
7975:
7974:
7958:
7955:
7954:
7928:
7924:
7912:
7908:
7897:
7894:
7893:
7865:
7862:
7861:
7839:
7835:
7823:
7819:
7814:
7811:
7810:
7793:
7789:
7787:
7784:
7783:
7766:
7762:
7760:
7757:
7756:
7737:
7709:
7703:
7691:
7684:
7677:
7670:
7663:
7649:
7641:
7638:
7625:
7624:
7622:
7611:
7608:
7603:
7602:
7600:
7591:
7585:
7521:
7517:
7508:
7504:
7502:
7499:
7498:
7462:
7458:
7456:
7453:
7452:
7418:
7412:
7389:
7381:
7352:superosculating
7328:
7315:
7281:
7277:
7268:
7264:
7262:
7259:
7258:
7230:
7227:
7226:
7203:
7199:
7190:
7186:
7184:
7181:
7180:
7174:
7171:
7159:
7155:
7151:
7141:
7137:
7133:
7122:
7118:
7107:
7104:
7097:
7095:
7088:
7087:
7083:
7079:
7076:
7070:
7067:
7061:
7054:
7053:
7049:
7045:
7042:
7036:
7033:
7027:
7020:
7019:
7018:). On the side
7012:
7011:
7001:
6998:
6993:
6992:
6990:
6989:
6982:
6981:
6974:
6973:
6969:
6962:
6961:
6950:
6915:
6909:
6898:
6895:
6890:
6889:
6887:
6878:
6875:
6870:
6869:
6867:
6866:
6850:
6846:
6839:
6838:
6831:
6830:
6826:
6819:
6818:
6811:
6810:
6806:
6799:
6798:
6791:
6790:
6786:
6779:
6778:
6771:
6770:
6766:
6759:
6758:
6754:
6732:
6722:
6696:
6684:
6678:
6666:
6648:
6634:
6628:
6622:
6612:
6599:
6595:
6574:
6568:
6536:
6509:
6506:
6505:
6475:
6472:
6471:
6451:
6448:
6447:
6418:
6415:
6414:
6389:
6386:
6385:
6369:
6366:
6365:
6332:
6329:
6328:
6303:
6300:
6299:
6283:
6280:
6279:
6255:
6252:
6251:
6235:
6232:
6231:
6209:
6206:
6205:
6165:
6162:
6161:
6138:
6132:
6119:
6096:
6092:
6088:
6080:
6076:
6068:
6064:
6061:absolute points
6042:
6018:
6013:
6012:
6010:
6007:
6006:
5975:
5941:
5940:
5935:
5930:
5924:
5923:
5918:
5913:
5907:
5906:
5901:
5896:
5889:
5885:
5877:
5874:
5873:
5841:
5837:
5795:
5791:
5764:
5760:
5755:
5752:
5751:
5714:
5713:
5707:
5706:
5700:
5699:
5692:
5688:
5681:
5680:
5675:
5667:
5662:
5654:
5648:
5647:
5639:
5634:
5629:
5621:
5615:
5614:
5606:
5601:
5593:
5588:
5581:
5577:
5570:
5569:
5564:
5559:
5552:
5548:
5546:
5543:
5542:
5509:
5505:
5469:
5465:
5441:
5437:
5432:
5429:
5428:
5418:
5397:
5378:
5355:
5315:
5296:
5227:Johannes Kepler
5210:
5184:cubic equations
5172:
5159:
5135:
5113:
5096:
5068:
5063:
5053:and to prevent
4971:
4952:
4945:
4937:
4930:
4921:
4915:
4876:
4871:
4863:
4860:
4859:
4850:
4831:
4809:
4805:
4799:
4795:
4787:
4784:
4783:
4763:
4760:
4759:
4730:
4726:
4718:
4670:
4666:
4664:
4661:
4660:
4639:
4638:
4633:
4625:
4619:
4618:
4610:
4605:
4598:
4594:
4592:
4589:
4588:
4567:
4563:
4561:
4558:
4557:
4540:
4536:
4534:
4531:
4530:
4492:
4488:
4480:
4473:
4467:
4456:
4455:
4454:
4452:
4434:
4430:
4422:
4415:
4409:
4398:
4397:
4396:
4394:
4392:
4389:
4388:
4350:
4345:
4335:
4331:
4323:
4316:
4310:
4299:
4298:
4297:
4295:
4280:
4276:
4270:
4265:
4253:
4246:
4240:
4229:
4228:
4227:
4225:
4223:
4220:
4219:
4194:
4193:
4179:
4178:
4176:
4173:
4172:
4121:
4117:
4093:
4089:
4084:
4081:
4080:
4074:
4068:
4038:
4034:
4032:
4015:
4012:
4011:
3970:
3966:
3942:
3938:
3920:
3916:
3892:
3888:
3883:
3880:
3879:
3869:
3861:
3832:
3828:
3819:
3815:
3801:
3779:
3770:
3766:
3757:
3753:
3739:
3735:
3732:
3724:
3721:
3720:
3705:
3651:
3647:
3623:
3619:
3614:
3611:
3610:
3604:
3589:
3583:
3565:
3554:
3541:
3538:
3529:
3525:
3521:
3517:
3496:
3478:
3460:
3444:
3434:
3416:
3385:
3384:
3379:
3371:
3365:
3364:
3356:
3351:
3344:
3340:
3338:
3335:
3334:
3327:
3323:
3290:
3286:
3284:
3281:
3280:
3277:
3242:
3241:
3235:
3234:
3228:
3227:
3217:
3216:
3209:
3208:
3203:
3195:
3190:
3182:
3176:
3175:
3167:
3162:
3157:
3149:
3143:
3142:
3134:
3129:
3121:
3116:
3106:
3105:
3098:
3097:
3092:
3087:
3077:
3076:
3074:
3071:
3070:
3038:
3037:
3031:
3030:
3020:
3019:
3012:
3011:
3006:
2996:
2995:
2985:
2984:
2978:
2977:
2967:
2966:
2959:
2958:
2953:
2945:
2939:
2938:
2930:
2925:
2915:
2914:
2907:
2906:
2901:
2891:
2890:
2888:
2885:
2884:
2881:
2875:
2873:Matrix notation
2866:
2809:
2805:
2781:
2777:
2772:
2769:
2768:
2746:
2713:
2702:
2684:
2674:
2670:
2668:
2665:
2664:
2602:
2564:
2561:
2560:
2516:
2512:
2504:
2501:
2500:
2442:
2439:
2438:
2380:
2377:
2376:
2350:
2340:
2334:
2328:
2322:
2297:
2293:
2282:
2279:
2278:
2244:
2240:
2234:
2230:
2228:
2217:
2213:
2207:
2203:
2201:
2199:
2196:
2195:
2161:
2140:
2136:
2134:
2131:
2130:
2096:
2092:
2086:
2082:
2080:
2069:
2065:
2059:
2055:
2053:
2051:
2048:
2047:
2021:
2017:
2008:
2004:
1995:
1991:
1989:
1986:
1985:
1967:
1955:
1945:
1924:
1916:
1912:
1898:
1883:
1876:
1862:
1848:
1844:
1836:
1828:
1824:
1781:
1754:
1750:
1741:
1737:
1730:
1726:
1724:
1722:
1719:
1718:
1695:
1691:
1689:
1687:
1684:
1683:
1663:
1659:
1650:
1646:
1644:
1642:
1639:
1638:
1616:
1612:
1606:
1602:
1600:
1592:
1590:
1587:
1586:
1560:
1556:
1550:
1546:
1544:
1533:
1529:
1523:
1519:
1517:
1515:
1512:
1511:
1483:
1480:
1479:
1458:
1455:
1454:
1433:
1430:
1429:
1398:
1394:
1392:
1389:
1388:
1360:
1356:
1347:
1343:
1336:
1332:
1330:
1328:
1325:
1324:
1301:
1297:
1295:
1293:
1290:
1289:
1269:
1265:
1256:
1252:
1250:
1248:
1245:
1244:
1222:
1218:
1212:
1208:
1206:
1198:
1196:
1193:
1192:
1166:
1162:
1156:
1152:
1150:
1139:
1135:
1129:
1125:
1123:
1121:
1118:
1117:
1093:
1090:
1089:
1071:
1068:
1067:
1049:
1046:
1045:
1027:
1024:
1023:
1004:
1000:
991:
987:
978:
974:
972:
969:
968:
953:
944:
935:
926:
886:
883:
882:
858:
841:
838:
837:
808:
805:
804:
775:
772:
771:
761:
757:
753:
750:semi-minor axis
738:
730:
722:
718:
714:
710:semi-major axis
697:
694:focal parameter
686:
667:
645:
634:
622:
615:
608:
601:
561:
550:
548:
546:
543:
542:
523:
520:
519:
503:
500:
499:
482:
475:
467:
459:
455:
445:
435:
431:
419:
411:
404:
397:
390:
379:
371:spherical conic
367:spheric section
298:
279:
272:
271:
265:
258:
257:
250:
183:
179:
155:
151:
146:
143:
142:
107:Euclidean plane
74:intersecting a
64:quadratic curve
28:
23:
22:
15:
12:
11:
5:
11182:
11172:
11171:
11166:
11161:
11156:
11151:
11149:Conic sections
11134:
11133:
11130:
11129:
11127:
11126:
11121:
11116:
11110:
11108:
11106:Vector bundles
11102:
11101:
11099:
11098:
11093:
11088:
11083:
11078:
11072:
11070:
11064:
11063:
11061:
11060:
11055:
11050:
11045:
11039:
11037:
11033:
11032:
11030:
11029:
11024:
11019:
11014:
11009:
11003:
11001:
10997:
10996:
10994:
10993:
10988:
10983:
10978:
10973:
10968:
10963:
10958:
10952:
10950:
10943:
10939:
10938:
10936:
10935:
10930:
10925:
10919:
10917:
10913:
10912:
10910:
10909:
10904:
10899:
10894:
10889:
10884:
10879:
10874:
10869:
10864:
10859:
10853:
10851:
10845:
10844:
10842:
10841:
10836:
10831:
10826:
10821:
10816:
10811:
10806:
10801:
10796:
10791:
10786:
10781:
10776:
10770:
10768:
10762:
10761:
10759:
10758:
10753:
10748:
10743:
10738:
10732:
10730:
10726:
10725:
10722:
10721:
10719:
10718:
10713:
10707:
10705:
10701:
10700:
10698:
10697:
10692:
10687:
10682:
10677:
10672:
10667:
10662:
10657:
10652:
10647:
10641:
10639:
10635:
10634:
10632:
10631:
10626:
10621:
10616:
10610:
10608:
10601:
10595:
10594:
10592:
10591:
10586:
10584:Riemann sphere
10581:
10576:
10571:
10565:
10563:
10557:
10556:
10548:
10547:
10540:
10533:
10525:
10519:
10518:
10512:
10491:
10490:External links
10488:
10487:
10486:
10477:
10472:
10459:
10454:
10434:Samuel, Pierre
10430:
10424:
10411:
10400:Addison-Wesley
10391:
10386:
10371:
10366:
10351:
10346:
10329:
10324:
10304:
10283:
10274:
10262:
10257:
10242:
10233:
10228:
10210:
10205:
10190:
10185:
10171:Boyer, Carl B.
10167:
10162:
10146:
10140:
10121:
10118:
10115:
10114:
10102:
10082:
10066:
10060:
10034:
10020:
9991:
9979:
9966:(7): 317–329,
9950:
9938:
9926:
9914:
9902:
9887:
9875:
9863:
9847:
9835:
9819:
9807:
9795:
9783:
9771:
9756:
9744:
9732:
9720:
9708:
9706:, p. 114.
9693:
9691:, p. 110.
9681:
9679:, p. 126.
9669:
9658:on 17 May 2013
9637:
9630:
9605:
9598:
9580:
9573:
9555:
9523:
9491:
9484:
9478:. p. 53.
9460:
9448:
9436:
9417:
9405:
9392:
9380:
9368:
9356:
9344:
9332:
9306:
9290:
9278:
9263:
9248:
9224:
9211:
9199:
9184:
9174:
9154:
9142:
9130:
9118:
9106:
9094:
9082:
9070:
9064:, p. 19;
9054:
9042:
9017:
9005:
8992:
8991:
8989:
8986:
8983:
8982:
8973:
8964:
8955:
8938:
8928:
8927:
8925:
8922:
8921:
8920:
8915:
8910:
8905:
8900:
8895:
8890:
8885:
8878:
8875:
8862:
8861:
8838:
8833:
8821:
8818:
8815:
8812:
8808:
8803:
8799:
8796:
8792:
8771:
8768:
8765:
8762:
8758:
8753:
8749:
8746:
8742:
8722:
8719:
8716:
8713:
8709:
8704:
8700:
8697:
8693:
8689:
8686:
8663:
8649:
8643:
8631:
8630:
8629:is hyperbolic.
8607:
8604:
8574:
8570:
8566:
8561:
8557:
8534:
8530:
8510:
8505:
8501:
8497:
8492:
8488:
8456:
8453:
8438:
8437:
8436:
8422:
8418:
8414:
8409:
8405:
8394:
8380:
8376:
8365:
8351:
8347:
8343:
8338:
8334:
8311:
8308:
8305:
8302:
8299:
8296:
8293:
8290:
8258:
8253:
8248:
8245:
8242:
8238:
8234:
8231:
8228:
8223:
8218:
8215:
8212:
8208:
8204:
8199:
8194:
8190:
8186:
8183:
8180:
8175:
8170:
8166:
8162:
8157:
8152:
8148:
8124:
8106:
8103:
8070:characteristic
8061:
8058:
8057:
8056:
8053:
8040:
8036:
8024:
8010:
8006:
7994:
7982:
7962:
7942:
7939:
7936:
7931:
7927:
7923:
7920:
7915:
7911:
7907:
7904:
7901:
7881:
7878:
7875:
7872:
7869:
7858:
7847:
7842:
7838:
7834:
7831:
7826:
7822:
7818:
7796:
7792:
7769:
7765:
7736:
7733:
7705:Main article:
7702:
7699:
7538:
7535:
7532:
7529:
7524:
7520:
7516:
7511:
7507:
7482:
7479:
7476:
7473:
7470:
7465:
7461:
7411:
7408:
7292:
7289:
7284:
7280:
7276:
7271:
7267:
7246:
7243:
7240:
7237:
7234:
7214:
7211:
7206:
7202:
7198:
7193:
7189:
7170:
7167:
7102:
7093:
7074:
7065:
7052:. On the side
7040:
7031:
6914:with vertices
6721:
6718:
6703:absolute point
6671:is called the
6570:Main article:
6567:
6564:
6535:
6532:
6519:
6516:
6513:
6479:
6455:
6431:
6428:
6425:
6422:
6413:onto a pencil
6402:
6399:
6396:
6393:
6373:
6358:
6357:
6345:
6342:
6339:
6336:
6316:
6313:
6310:
6307:
6287:
6259:
6239:
6219:
6216:
6213:
6193:
6190:
6187:
6184:
6181:
6178:
6175:
6172:
6169:
6134:Main article:
6131:
6128:
6041:
6038:
6026:
6021:
6016:
5962:
5961:
5950:
5946:
5939:
5936:
5934:
5931:
5929:
5926:
5925:
5922:
5919:
5917:
5914:
5912:
5909:
5908:
5905:
5902:
5900:
5897:
5895:
5892:
5891:
5888:
5884:
5881:
5867:
5866:
5855:
5852:
5849:
5844:
5840:
5836:
5833:
5830:
5827:
5824:
5821:
5818:
5815:
5812:
5809:
5806:
5803:
5798:
5794:
5790:
5787:
5784:
5781:
5778:
5775:
5772:
5767:
5763:
5759:
5738:
5737:
5726:
5723:
5719:
5712:
5709:
5708:
5705:
5702:
5701:
5698:
5695:
5694:
5691:
5686:
5679:
5676:
5674:
5670:
5666:
5663:
5661:
5657:
5653:
5650:
5649:
5646:
5642:
5638:
5635:
5633:
5630:
5628:
5624:
5620:
5617:
5616:
5613:
5609:
5605:
5602:
5600:
5596:
5592:
5589:
5587:
5584:
5583:
5580:
5575:
5568:
5565:
5563:
5560:
5558:
5555:
5554:
5551:
5532:
5531:
5520:
5517:
5512:
5508:
5504:
5501:
5498:
5495:
5492:
5489:
5486:
5483:
5480:
5477:
5472:
5468:
5464:
5461:
5458:
5455:
5452:
5449:
5444:
5440:
5436:
5417:
5414:
5396:
5393:
5368:quadratic form
5354:
5351:
5331:center of mass
5295:
5292:
5255:René Descartes
5209:
5206:
5171:
5168:
5141:Conic Sections
5112:
5109:
5067:
5064:
5062:
5059:
5021:exterior point
5017:interior point
4970:
4967:
4929:As above, for
4912:
4911:
4900:
4894:
4891:
4888:
4885:
4882:
4879:
4875:
4870:
4867:
4830:
4827:
4812:
4808:
4802:
4798:
4794:
4791:
4767:
4756:
4755:
4744:
4741:
4738:
4733:
4729:
4725:
4721:
4717:
4714:
4711:
4708:
4705:
4702:
4699:
4696:
4693:
4690:
4687:
4684:
4681:
4678:
4673:
4669:
4644:
4637:
4634:
4632:
4628:
4624:
4621:
4620:
4617:
4613:
4609:
4606:
4604:
4601:
4600:
4597:
4587:of the matrix
4570:
4566:
4543:
4539:
4527:
4526:
4515:
4512:
4509:
4503:
4500:
4495:
4491:
4487:
4483:
4479:
4476:
4470:
4463:
4460:
4451:
4445:
4442:
4437:
4433:
4429:
4425:
4421:
4418:
4412:
4405:
4402:
4382:
4381:
4370:
4367:
4364:
4358:
4353:
4348:
4344:
4338:
4334:
4330:
4326:
4322:
4319:
4313:
4306:
4303:
4294:
4288:
4283:
4279:
4273:
4268:
4264:
4260:
4256:
4252:
4249:
4243:
4236:
4233:
4201:
4198:
4192:
4186:
4183:
4169:
4168:
4156:
4153:
4150:
4147:
4144:
4141:
4138:
4135:
4132:
4129:
4124:
4120:
4116:
4113:
4110:
4107:
4104:
4101:
4096:
4092:
4088:
4067:
4064:
4051:
4046:
4041:
4037:
4031:
4028:
4025:
4022:
4019:
4008:
4007:
3996:
3993:
3990:
3987:
3984:
3981:
3978:
3973:
3969:
3965:
3962:
3959:
3956:
3953:
3950:
3945:
3941:
3937:
3934:
3931:
3928:
3923:
3919:
3915:
3912:
3909:
3906:
3903:
3900:
3895:
3891:
3887:
3858:
3857:
3846:
3835:
3831:
3827:
3822:
3818:
3814:
3811:
3808:
3805:
3800:
3797:
3794:
3791:
3788:
3785:
3782:
3773:
3769:
3765:
3760:
3756:
3752:
3749:
3746:
3743:
3738:
3731:
3728:
3702:
3701:
3689:
3686:
3683:
3680:
3677:
3674:
3671:
3668:
3665:
3662:
3659:
3654:
3650:
3646:
3643:
3640:
3637:
3634:
3631:
3626:
3622:
3618:
3603:
3600:
3537:
3534:
3514:
3513:
3512:
3511:
3475:
3457:
3456:
3455:
3409:non-degenerate
3394:
3390:
3383:
3380:
3378:
3374:
3370:
3367:
3366:
3363:
3359:
3355:
3352:
3350:
3347:
3346:
3343:
3307:
3304:
3301:
3298:
3293:
3289:
3276:
3273:
3254:
3251:
3246:
3240:
3237:
3236:
3233:
3230:
3229:
3226:
3223:
3222:
3220:
3213:
3207:
3204:
3202:
3198:
3194:
3191:
3189:
3185:
3181:
3178:
3177:
3174:
3170:
3166:
3163:
3161:
3158:
3156:
3152:
3148:
3145:
3144:
3141:
3137:
3133:
3130:
3128:
3124:
3120:
3117:
3115:
3112:
3111:
3109:
3102:
3096:
3093:
3091:
3088:
3086:
3083:
3082:
3080:
3056:
3053:
3050:
3047:
3042:
3036:
3033:
3032:
3029:
3026:
3025:
3023:
3016:
3010:
3007:
3005:
3002:
3001:
2999:
2994:
2989:
2983:
2980:
2979:
2976:
2973:
2972:
2970:
2963:
2957:
2954:
2952:
2948:
2944:
2941:
2940:
2937:
2933:
2929:
2926:
2924:
2921:
2920:
2918:
2911:
2905:
2902:
2900:
2897:
2896:
2894:
2877:Main article:
2874:
2871:
2869:not all zero.
2859:
2858:
2847:
2844:
2841:
2838:
2835:
2832:
2829:
2826:
2823:
2820:
2817:
2812:
2808:
2804:
2801:
2798:
2795:
2792:
2789:
2784:
2780:
2776:
2745:
2742:
2741:
2740:
2739:
2738:
2727:
2721:
2717:
2712:
2709:
2701:
2697:
2691:
2688:
2683:
2680:
2677:
2673:
2656:
2655:
2654:
2642:
2639:
2636:
2633:
2630:
2627:
2624:
2621:
2618:
2615:
2612:
2609:
2604: or
2601:
2598:
2595:
2592:
2589:
2586:
2583:
2580:
2577:
2574:
2571:
2568:
2552:
2551:
2550:
2539:
2536:
2533:
2530:
2527:
2524:
2519:
2515:
2511:
2508:
2492:
2491:
2490:
2479:
2476:
2473:
2470:
2467:
2464:
2461:
2458:
2455:
2452:
2449:
2446:
2430:
2429:
2428:
2417:
2414:
2411:
2408:
2405:
2402:
2399:
2396:
2393:
2390:
2387:
2384:
2364:parametrically
2319:
2318:
2317:
2316:
2305:
2300:
2296:
2292:
2289:
2286:
2273:
2272:
2271:
2260:
2257:
2254:
2247:
2243:
2237:
2233:
2227:
2220:
2216:
2210:
2206:
2190:
2189:
2188:
2177:
2174:
2171:
2168:
2160:
2157:
2154:
2151:
2148:
2143:
2139:
2125:
2124:
2123:
2112:
2109:
2106:
2099:
2095:
2089:
2085:
2079:
2072:
2068:
2062:
2058:
2042:
2041:
2040:
2029:
2024:
2020:
2016:
2011:
2007:
2003:
1998:
1994:
1821:standard forms
1780:
1777:
1774:
1773:
1757:
1753:
1749:
1744:
1740:
1733:
1729:
1716:
1703:
1698:
1694:
1681:
1666:
1662:
1658:
1653:
1649:
1636:
1619:
1615:
1609:
1605:
1599:
1596:
1584:
1573:
1570:
1563:
1559:
1553:
1549:
1543:
1536:
1532:
1526:
1522:
1509:
1503:
1502:
1490:
1487:
1477:
1465:
1462:
1452:
1449:
1437:
1427:
1415:
1412:
1409:
1406:
1401:
1397:
1386:
1380:
1379:
1363:
1359:
1355:
1350:
1346:
1339:
1335:
1322:
1309:
1304:
1300:
1287:
1272:
1268:
1264:
1259:
1255:
1242:
1225:
1221:
1215:
1211:
1205:
1202:
1190:
1179:
1176:
1169:
1165:
1159:
1155:
1149:
1142:
1138:
1132:
1128:
1115:
1109:
1108:
1097:
1087:
1075:
1065:
1053:
1043:
1031:
1021:
1007:
1003:
999:
994:
990:
986:
981:
977:
966:
960:
959:
950:
941:
932:
925:eccentricity (
923:
920:
919:conic section
902:
899:
896:
893:
890:
879:
878:
865:
862:
857:
854:
851:
848:
835:
824:
821:
818:
815:
802:
791:
788:
785:
782:
741:non-negative.
653:principal axis
633:
630:
576:
570:
567:
564:
559:
556:
553:
530:
527:
507:
430:of all points
378:
375:
297:
294:
249:
246:
218:
215:
212:
209:
206:
203:
200:
197:
194:
191:
186:
182:
178:
175:
172:
169:
166:
163:
158:
154:
150:
72:cone's surface
26:
18:Conic sections
9:
6:
4:
3:
2:
11181:
11170:
11167:
11165:
11162:
11160:
11157:
11155:
11152:
11150:
11147:
11146:
11144:
11125:
11122:
11120:
11117:
11115:
11112:
11111:
11109:
11107:
11103:
11097:
11094:
11092:
11089:
11087:
11084:
11082:
11079:
11077:
11074:
11073:
11071:
11069:
11068:Singularities
11065:
11059:
11056:
11054:
11051:
11049:
11046:
11044:
11041:
11040:
11038:
11034:
11028:
11025:
11023:
11020:
11018:
11015:
11013:
11010:
11008:
11005:
11004:
11002:
10998:
10992:
10989:
10987:
10984:
10982:
10979:
10977:
10974:
10972:
10969:
10967:
10964:
10962:
10959:
10957:
10954:
10953:
10951:
10947:
10944:
10940:
10934:
10931:
10929:
10926:
10924:
10921:
10920:
10918:
10916:Constructions
10914:
10908:
10905:
10903:
10900:
10898:
10895:
10893:
10890:
10888:
10887:Klein quartic
10885:
10883:
10880:
10878:
10875:
10873:
10870:
10868:
10867:Bolza surface
10865:
10863:
10862:Bring's curve
10860:
10858:
10855:
10854:
10852:
10850:
10846:
10840:
10837:
10835:
10832:
10830:
10827:
10825:
10822:
10820:
10817:
10815:
10812:
10810:
10807:
10805:
10802:
10800:
10797:
10795:
10794:Conic section
10792:
10790:
10787:
10785:
10782:
10780:
10777:
10775:
10774:AF+BG theorem
10772:
10771:
10769:
10767:
10763:
10757:
10754:
10752:
10749:
10747:
10744:
10742:
10739:
10737:
10734:
10733:
10731:
10727:
10717:
10714:
10712:
10709:
10708:
10706:
10702:
10696:
10693:
10691:
10688:
10686:
10683:
10681:
10678:
10676:
10673:
10671:
10668:
10666:
10663:
10661:
10658:
10656:
10653:
10651:
10648:
10646:
10643:
10642:
10640:
10636:
10630:
10627:
10625:
10622:
10620:
10617:
10615:
10612:
10611:
10609:
10605:
10602:
10600:
10596:
10590:
10589:Twisted cubic
10587:
10585:
10582:
10580:
10577:
10575:
10572:
10570:
10567:
10566:
10564:
10562:
10558:
10554:
10546:
10541:
10539:
10534:
10532:
10527:
10526:
10523:
10516:
10513:
10508:
10507:
10502:
10499:
10494:
10493:
10483:
10478:
10475:
10473:0-201-07540-7
10469:
10465:
10460:
10457:
10455:0-387-96752-4
10451:
10447:
10442:
10441:
10435:
10431:
10427:
10425:9783642172854
10421:
10417:
10412:
10409:
10405:
10401:
10397:
10392:
10389:
10387:0-486-63415-9
10383:
10379:
10378:
10372:
10369:
10367:9780486154893
10363:
10359:
10358:
10352:
10349:
10343:
10339:
10335:
10330:
10327:
10321:
10316:
10315:
10309:
10305:
10291:
10290:
10284:
10280:
10275:
10271:
10267:
10263:
10260:
10258:0-486-42876-1
10254:
10250:
10249:
10243:
10239:
10234:
10231:
10229:9780387406237
10225:
10222:, Blaisdell,
10221:
10220:
10215:
10211:
10208:
10202:
10198:
10197:
10191:
10188:
10182:
10178:
10177:
10172:
10168:
10165:
10159:
10155:
10151:
10150:Artzy, Rafael
10147:
10143:
10137:
10133:
10129:
10124:
10123:
10112:, p. 196
10111:
10106:
10099:
10095:
10091:
10086:
10079:
10075:
10074:Faulkner 1952
10070:
10063:
10061:0-486-60288-5
10057:
10053:
10048:
10047:
10038:
10030:
10024:
10017:
10013:
10009:
10005:
10001:
9995:
9988:
9983:
9974:
9969:
9965:
9961:
9954:
9947:
9942:
9935:
9930:
9923:
9918:
9911:
9906:
9900:
9896:
9895:Faulkner 1952
9891:
9884:
9879:
9872:
9867:
9860:
9856:
9855:Faulkner 1952
9851:
9844:
9839:
9832:
9828:
9823:
9816:
9815:Merserve 1983
9811:
9804:
9799:
9792:
9787:
9781:, p. 320
9780:
9775:
9769:
9765:
9764:Faulkner 1952
9760:
9753:
9752:Faulkner 1952
9748:
9741:
9736:
9729:
9724:
9717:
9712:
9705:
9700:
9698:
9690:
9685:
9678:
9673:
9654:
9647:
9641:
9633:
9627:
9623:
9619:
9615:
9609:
9601:
9595:
9591:
9584:
9576:
9570:
9566:
9559:
9552:
9548:
9544:
9540:
9536:
9532:
9527:
9520:
9516:
9512:
9508:
9504:
9500:
9495:
9487:
9485:0-292-78149-0
9481:
9477:
9473:
9472:
9464:
9458:, p. 36.
9457:
9452:
9446:, p. 30.
9445:
9440:
9433:
9429:
9428:
9421:
9414:
9409:
9402:
9399:Heath, T.L.,
9396:
9390:, p. 117
9389:
9384:
9377:
9372:
9365:
9360:
9353:
9348:
9341:
9336:
9328:
9324:
9317:
9310:
9303:
9299:
9294:
9287:
9282:
9275:
9274:
9267:
9260:
9259:
9252:
9245:
9241:
9240:
9233:
9231:
9229:
9221:
9215:
9209:, p. 153
9208:
9203:
9197:, p. 326
9196:
9191:
9189:
9182:
9177:
9175:0-471-75715-2
9171:
9167:
9166:
9158:
9151:
9146:
9140:, p. 316
9139:
9134:
9128:, p. 130
9127:
9122:
9115:
9110:
9103:
9098:
9091:
9086:
9079:
9074:
9067:
9063:
9058:
9052:, p. 434
9051:
9046:
9039:
9035:
9031:
9027:
9021:
9014:
9009:
9003:, p. 319
9002:
8997:
8993:
8977:
8968:
8959:
8952:
8948:
8945:According to
8942:
8933:
8929:
8919:
8916:
8914:
8911:
8909:
8906:
8904:
8901:
8899:
8896:
8894:
8891:
8889:
8886:
8884:
8881:
8880:
8871:
8866:
8859:
8855:
8851:
8847:
8843:
8839:
8837:
8834:
8819:
8816:
8813:
8810:
8806:
8797:
8794:
8769:
8766:
8763:
8760:
8756:
8747:
8744:
8720:
8717:
8714:
8711:
8707:
8698:
8695:
8687:
8684:
8676:
8672:
8669:
8658:
8655:
8644:
8642:
8639:
8638:
8637:
8635:
8628:
8627:wave equation
8624:
8623:heat equation
8620:
8615:
8611:
8608:
8605:
8602:
8598:
8594:
8590:
8572:
8568:
8564:
8559:
8555:
8532:
8528:
8508:
8503:
8499:
8495:
8490:
8486:
8477:
8473:
8469:
8465:
8461:
8457:
8454:
8451:
8447:
8443:
8439:
8420:
8416:
8412:
8407:
8403:
8395:
8378:
8374:
8366:
8349:
8345:
8341:
8336:
8332:
8324:
8323:
8309:
8306:
8303:
8300:
8297:
8294:
8291:
8288:
8280:
8276:
8272:
8256:
8251:
8246:
8243:
8240:
8236:
8232:
8229:
8226:
8221:
8216:
8213:
8210:
8206:
8202:
8197:
8192:
8188:
8184:
8181:
8178:
8173:
8168:
8164:
8160:
8155:
8150:
8146:
8137:
8136:diagonal form
8133:
8129:
8125:
8123:
8120:
8119:
8118:
8115:
8113:
8102:
8100:
8096:
8095:elliptic cone
8091:
8089:
8084:
8082:
8077:
8075:
8071:
8067:
8054:
8038:
8034:
8025:
8008:
8004:
7995:
7980:
7960:
7940:
7937:
7929:
7925:
7921:
7918:
7913:
7909:
7905:
7876:
7873:
7870:
7859:
7845:
7840:
7836:
7832:
7829:
7824:
7820:
7816:
7794:
7790:
7767:
7763:
7754:
7753:
7752:
7749:
7747:
7743:
7732:
7730:
7726:
7722:
7718:
7714:
7708:
7698:
7694:
7687:
7680:
7673:
7666:
7660:
7656:
7652:
7636:
7632:
7628:
7620:
7606:
7598:
7594:
7588:
7582:
7580:
7574:
7572:
7568:
7562:
7560:
7556:
7552:
7536:
7533:
7530:
7527:
7522:
7518:
7514:
7509:
7505:
7496:
7480:
7477:
7474:
7471:
7468:
7463:
7459:
7450:
7446:
7441:
7439:
7438:straight line
7435:
7431:
7426:
7423:
7417:
7407:
7405:
7403:
7399:
7393:
7385:
7380:
7379:cyclic points
7376:
7372:
7368:
7364:
7360:
7359:straight line
7355:
7353:
7349:
7345:
7340:
7336:
7331:
7325:
7323:
7318:
7314:
7309:
7306:
7290:
7287:
7282:
7278:
7274:
7269:
7265:
7244:
7241:
7238:
7235:
7232:
7212:
7209:
7204:
7200:
7196:
7191:
7187:
7177:
7166:
7163:
7148:
7144:
7129:
7125:
7115:
7111:
7100:
7091:
7073:
7064:
7057:
7039:
7030:
7023:
7015:
7004:
6996:
6985:
6977:
6965:
6957:
6953:
6946:
6942:
6938:
6934:
6930:
6926:
6922:
6918:
6912:
6901:
6893:
6881:
6873:
6858:
6854:
6842:
6834:
6822:
6814:
6802:
6794:
6782:
6774:
6762:
6751:
6747:
6743:
6739:
6735:
6730:
6725:
6720:Constructions
6717:
6715:
6714:Steiner conic
6710:
6708:
6704:
6699:
6694:
6693:
6687:
6681:
6676:
6675:
6669:
6664:
6659:
6655:
6651:
6645:
6641:
6637:
6631:
6625:
6620:
6615:
6610:
6607:
6602:
6593:
6588:
6586:
6582:
6578:
6573:
6563:
6561:
6555:
6553:
6549:
6545:
6541:
6531:
6517:
6514:
6511:
6503:
6502:pappian plane
6498:
6496:
6491:
6477:
6469:
6453:
6445:
6426:
6420:
6397:
6391:
6371:
6363:
6340:
6334:
6311:
6305:
6285:
6277:
6273:
6270:resp.) and a
6257:
6237:
6217:
6214:
6211:
6188:
6182:
6179:
6173:
6167:
6159:
6158:
6157:
6155:
6154:Jakob Steiner
6151:
6142:
6137:
6136:Steiner conic
6127:
6122:
6115:
6113:
6109:
6105:
6100:
6086:
6083:which is the
6074:
6062:
6058:
6057:absolute line
6053:
6051:
6046:
6037:
6024:
6019:
6005:
5999:
5995:
5991:
5987:
5983:
5979:
5972:
5970:
5965:
5948:
5944:
5937:
5932:
5927:
5920:
5915:
5910:
5903:
5898:
5893:
5886:
5882:
5879:
5872:
5871:
5870:
5853:
5850:
5847:
5842:
5838:
5834:
5831:
5828:
5825:
5822:
5819:
5816:
5813:
5810:
5807:
5804:
5801:
5796:
5792:
5788:
5785:
5782:
5779:
5776:
5773:
5770:
5765:
5761:
5757:
5750:
5749:
5748:
5745:
5743:
5724:
5721:
5717:
5710:
5703:
5696:
5689:
5684:
5677:
5672:
5668:
5664:
5659:
5655:
5651:
5644:
5640:
5636:
5631:
5626:
5622:
5618:
5611:
5607:
5603:
5598:
5594:
5590:
5585:
5578:
5573:
5566:
5561:
5556:
5549:
5541:
5540:
5539:
5537:
5518:
5515:
5510:
5506:
5502:
5499:
5496:
5493:
5490:
5487:
5484:
5481:
5478:
5475:
5470:
5466:
5462:
5459:
5456:
5453:
5450:
5447:
5442:
5438:
5434:
5427:
5426:
5425:
5423:
5413:
5411:
5405:
5402:
5392:
5390:
5386:
5381:
5375:
5373:
5369:
5365:
5361:
5350:
5348:
5344:
5338:
5336:
5332:
5328:
5324:
5320:
5313:
5309:
5305:
5301:
5291:
5288:
5283:
5278:
5273:
5268:
5264:
5260:
5259:Pierre Fermat
5256:
5252:
5250:
5246:
5242:
5241:Blaise Pascal
5238:
5234:
5232:
5228:
5221:
5220:
5214:
5205:
5203:
5198:
5196:
5192:
5187:
5185:
5181:
5177:
5170:Islamic world
5167:
5165:
5154:
5150:
5147:
5146:
5142:
5130:
5122:
5117:
5108:
5106:
5102:
5091:
5087:
5083:
5081:
5077:
5073:
5058:
5056:
5052:
5048:
5043:
5041:
5036:
5032:
5029:
5024:
5022:
5018:
5014:
5013:tangent lines
5009:
5007:
5003:
4999:
4994:
4990:
4988:
4984:
4980:
4976:
4966:
4964:
4959:
4958:a hyperbola.
4955:
4948:
4941:
4933:
4927:
4924:
4918:
4898:
4892:
4889:
4886:
4883:
4880:
4877:
4873:
4868:
4865:
4858:
4857:
4856:
4853:
4848:
4840:
4835:
4826:
4810:
4806:
4800:
4796:
4792:
4781:
4765:
4742:
4739:
4731:
4723:
4719:
4715:
4709:
4706:
4703:
4697:
4694:
4688:
4685:
4682:
4676:
4671:
4667:
4659:
4658:
4657:
4642:
4635:
4630:
4626:
4622:
4615:
4611:
4607:
4602:
4595:
4586:
4568:
4564:
4541:
4537:
4513:
4510:
4507:
4493:
4489:
4481:
4477:
4474:
4468:
4458:
4449:
4435:
4431:
4423:
4419:
4416:
4410:
4400:
4387:
4386:
4385:
4368:
4365:
4362:
4351:
4346:
4342:
4336:
4332:
4324:
4320:
4317:
4311:
4301:
4292:
4281:
4277:
4271:
4266:
4262:
4254:
4250:
4247:
4241:
4231:
4218:
4217:
4216:
4196:
4190:
4181:
4154:
4151:
4148:
4145:
4142:
4139:
4136:
4133:
4130:
4127:
4122:
4118:
4114:
4111:
4108:
4105:
4102:
4099:
4094:
4090:
4086:
4079:
4078:
4077:
4073:
4063:
4049:
4044:
4039:
4035:
4029:
4026:
4023:
4020:
3994:
3991:
3988:
3979:
3976:
3971:
3963:
3960:
3957:
3948:
3943:
3939:
3929:
3926:
3921:
3913:
3910:
3907:
3898:
3893:
3889:
3878:
3877:
3876:
3873:
3867:
3844:
3833:
3829:
3825:
3820:
3812:
3809:
3806:
3798:
3792:
3789:
3786:
3780:
3771:
3767:
3763:
3758:
3750:
3747:
3744:
3736:
3729:
3726:
3719:
3718:
3717:
3713:
3709:
3687:
3684:
3681:
3678:
3675:
3672:
3669:
3666:
3663:
3660:
3657:
3652:
3648:
3644:
3641:
3638:
3635:
3632:
3629:
3624:
3620:
3616:
3609:
3608:
3607:
3599:
3596:
3592:
3586:
3581:
3577:
3572:
3568:
3561:
3557:
3553:
3548:
3544:
3533:
3509:
3503:
3499:
3494:
3493:
3491:
3485:
3481:
3476:
3473:
3467:
3463:
3458:
3453:
3447:
3441:
3437:
3432:
3431:
3429:
3423:
3419:
3414:
3413:
3412:
3410:
3405:
3392:
3388:
3381:
3376:
3372:
3368:
3361:
3357:
3353:
3348:
3341:
3333:
3321:
3318:, called the
3305:
3302:
3299:
3296:
3291:
3287:
3272:
3270:
3265:
3252:
3249:
3244:
3238:
3231:
3224:
3218:
3211:
3205:
3200:
3196:
3192:
3187:
3183:
3179:
3172:
3168:
3164:
3159:
3154:
3150:
3146:
3139:
3135:
3131:
3126:
3122:
3118:
3113:
3107:
3100:
3094:
3089:
3084:
3078:
3067:
3054:
3051:
3048:
3045:
3040:
3034:
3027:
3021:
3014:
3008:
3003:
2997:
2992:
2987:
2981:
2974:
2968:
2961:
2955:
2950:
2946:
2942:
2935:
2931:
2927:
2922:
2916:
2909:
2903:
2898:
2892:
2880:
2870:
2864:
2845:
2842:
2839:
2836:
2833:
2830:
2827:
2824:
2821:
2818:
2815:
2810:
2806:
2802:
2799:
2796:
2793:
2790:
2787:
2782:
2778:
2774:
2767:
2766:
2765:
2763:
2759:
2755:
2751:
2725:
2719:
2715:
2710:
2707:
2699:
2695:
2689:
2686:
2681:
2678:
2675:
2671:
2663:
2662:
2660:
2657:
2637:
2634:
2631:
2628:
2625:
2622:
2619:
2616:
2613:
2610:
2599:
2593:
2590:
2587:
2584:
2581:
2578:
2575:
2572:
2569:
2559:
2558:
2556:
2553:
2537:
2531:
2528:
2525:
2522:
2517:
2513:
2509:
2499:
2498:
2496:
2493:
2477:
2471:
2468:
2465:
2462:
2459:
2456:
2453:
2450:
2447:
2437:
2436:
2434:
2431:
2415:
2409:
2406:
2403:
2400:
2397:
2394:
2391:
2388:
2385:
2375:
2374:
2372:
2369:
2368:
2367:
2365:
2360:
2357:
2353:
2347:
2343:
2337:
2331:
2325:
2303:
2298:
2294:
2290:
2287:
2284:
2277:
2276:
2274:
2258:
2255:
2252:
2245:
2241:
2235:
2231:
2225:
2218:
2214:
2208:
2204:
2194:
2193:
2191:
2175:
2172:
2169:
2166:
2158:
2155:
2152:
2149:
2146:
2141:
2137:
2129:
2128:
2126:
2110:
2107:
2104:
2097:
2093:
2087:
2083:
2077:
2070:
2066:
2060:
2056:
2046:
2045:
2043:
2027:
2022:
2018:
2014:
2009:
2005:
2001:
1996:
1992:
1984:
1983:
1981:
1980:
1979:
1975:
1971:
1963:
1959:
1952:
1948:
1943:
1939:
1934:
1931:
1927:
1920:
1909:
1905:
1901:
1897:
1896:
1890:
1886:
1879:
1873:
1869:
1865:
1859:
1855:
1851:
1840:
1835:and the foci
1832:
1822:
1818:
1814:
1810:
1801:
1793:
1785:
1755:
1751:
1747:
1742:
1738:
1731:
1727:
1717:
1701:
1696:
1692:
1682:
1664:
1660:
1656:
1651:
1647:
1637:
1617:
1613:
1607:
1603:
1597:
1594:
1585:
1571:
1568:
1561:
1557:
1551:
1547:
1541:
1534:
1530:
1524:
1520:
1510:
1508:
1505:
1504:
1488:
1485:
1478:
1463:
1460:
1453:
1450:
1435:
1428:
1413:
1410:
1407:
1404:
1399:
1395:
1387:
1385:
1382:
1381:
1361:
1357:
1353:
1348:
1344:
1337:
1333:
1323:
1307:
1302:
1298:
1288:
1270:
1266:
1262:
1257:
1253:
1243:
1223:
1219:
1213:
1209:
1203:
1200:
1191:
1177:
1174:
1167:
1163:
1157:
1153:
1147:
1140:
1136:
1130:
1126:
1116:
1114:
1111:
1110:
1088:
1073:
1066:
1051:
1044:
1029:
1022:
1005:
1001:
997:
992:
988:
984:
979:
975:
967:
965:
962:
961:
956:
951:
947:
942:
938:
933:
929:
924:
921:
918:
917:
914:
900:
897:
894:
891:
888:
863:
860:
855:
852:
849:
846:
836:
822:
819:
816:
813:
803:
789:
786:
783:
780:
770:
769:
768:
765:
751:
747:
742:
734:
726:
712:
711:
706:
701:
695:
690:
684:
680:
676:
671:
665:
660:
658:
654:
649:
638:
629:
626:
618:
612:
605:
598:
596:
592:
587:
574:
568:
565:
562:
557:
554:
551:
528:
525:
505:
496:
493:
489:
488:a hyperbola.
485:
478:
471:
465:
453:
452:
443:
442:
429:
417:
416:infinitesimal
407:
400:
393:
388:
383:
374:
372:
368:
365:Compare also
363:
361:
357:
353:
349:
345:
341:
337:
333:
329:
324:
322:
320:
315:
311:
307:
306:cutting plane
304:, called the
303:
293:
291:
283:
276:
269:
262:
254:
245:
243:
239:
235:
230:
216:
213:
210:
207:
204:
201:
198:
195:
192:
189:
184:
180:
176:
173:
170:
167:
164:
161:
156:
152:
148:
140:
136:
132:
128:
127:
122:
118:
117:
112:
108:
103:
101:
97:
93:
89:
85:
81:
77:
73:
69:
65:
61:
57:
56:conic section
48:
40:
32:
19:
11053:Prym variety
11027:Stable curve
11017:Hodge bundle
11007:ELSV formula
10809:Fermat curve
10793:
10766:Plane curves
10729:Higher genus
10704:Applications
10629:Modular form
10504:
10481:
10463:
10439:
10418:. Springer.
10415:
10395:
10376:
10356:
10333:
10313:
10298:20 September
10296:, retrieved
10288:
10278:
10269:
10266:Eves, Howard
10247:
10237:
10218:
10195:
10175:
10153:
10127:
10120:Bibliography
10105:
10093:
10085:
10069:
10045:
10037:
10023:
10003:
9994:
9982:
9963:
9959:
9953:
9948:, p. 70
9941:
9936:, p. 19
9929:
9924:, p. 14
9917:
9905:
9890:
9885:, p. 80
9883:Coxeter 1964
9878:
9873:, p. 60
9871:Coxeter 1964
9866:
9850:
9838:
9826:
9822:
9810:
9798:
9793:, p. 80
9791:Coxeter 1993
9786:
9774:
9759:
9754:, p. 71
9747:
9735:
9723:
9718:, p. 27
9711:
9684:
9672:
9660:. Retrieved
9653:the original
9640:
9617:
9608:
9589:
9583:
9564:
9558:
9534:
9526:
9506:
9499:Boyer, C. B.
9494:
9470:
9463:
9451:
9439:
9430:, edited by
9426:
9420:
9415:, p. 28
9408:
9400:
9395:
9383:
9378:, p. 18
9371:
9359:
9347:
9342:, p. 28
9335:
9326:
9322:
9309:
9301:
9293:
9288:, p. 17
9281:
9271:
9266:
9256:
9251:
9238:
9219:
9214:
9202:
9164:
9157:
9152:, p. 30
9145:
9133:
9121:
9109:
9097:
9085:
9073:
9057:
9045:
9025:
9020:
9015:, p. 13
9008:
8996:
8976:
8967:
8958:
8941:
8932:
8667:
8653:
8632:
8614:second order
8449:
8445:
8441:
8278:
8274:
8270:
8131:
8116:
8112:discriminant
8108:
8092:
8085:
8078:
8063:
7750:
7738:
7724:
7720:
7710:
7692:
7685:
7678:
7671:
7664:
7658:
7654:
7650:
7634:
7630:
7626:
7618:
7604:
7596:
7592:
7586:
7583:
7575:
7570:
7563:
7559:multiplicity
7554:
7494:
7442:
7427:
7421:
7419:
7406:
7391:
7383:
7363:tangent line
7356:
7351:
7339:intersection
7335:multiplicity
7329:
7326:
7316:
7310:
7175:
7172:
7164:
7146:
7142:
7127:
7123:
7113:
7109:
7098:
7089:
7078:starting at
7071:
7062:
7055:
7044:starting at
7037:
7028:
7021:
7013:
7002:
6994:
6983:
6975:
6963:
6955:
6951:
6944:
6940:
6936:
6932:
6928:
6924:
6920:
6916:
6910:
6899:
6891:
6879:
6871:
6863:
6840:
6832:
6820:
6812:
6800:
6792:
6780:
6772:
6760:
6749:
6745:
6741:
6737:
6733:
6728:
6726:
6723:
6711:
6706:
6702:
6697:
6691:
6685:
6679:
6673:
6667:
6661:. Following
6657:
6653:
6649:
6643:
6639:
6635:
6629:
6627:with a line
6623:
6613:
6600:
6591:
6589:
6584:
6580:
6575:
6559:
6556:
6551:
6547:
6543:
6537:
6499:
6494:
6492:
6467:
6384:of a pencil
6361:
6359:
6147:
6120:
6116:
6103:
6101:
6072:
6060:
6056:
6054:
6043:
5997:
5993:
5989:
5985:
5981:
5977:
5973:
5966:
5963:
5868:
5746:
5741:
5739:
5533:
5419:
5410:double point
5406:
5398:
5379:
5376:
5356:
5339:
5316:
5294:Applications
5253:
5235:
5225:
5217:
5199:
5188:
5180:Omar Khayyám
5173:
5151:
5144:
5140:
5126:
5120:
5104:
5100:
5084:
5069:
5051:laminar flow
5044:
5033:
5027:
5025:
5020:
5016:
5010:
5005:
5001:
4997:
4995:
4991:
4972:
4960:
4953:
4946:
4939:
4931:
4928:
4922:
4916:
4913:
4851:
4844:
4838:
4757:
4528:
4383:
4170:
4075:
4010:where again
4009:
3874:
3859:
3711:
3707:
3703:
3605:
3594:
3590:
3588:and the sum
3584:
3570:
3566:
3559:
3555:
3546:
3542:
3539:
3515:
3501:
3497:
3483:
3479:
3465:
3461:
3445:
3439:
3435:
3421:
3417:
3406:
3320:discriminant
3278:
3275:Discriminant
3266:
3068:
2882:
2863:real numbers
2860:
2747:
2361:
2355:
2351:
2345:
2341:
2335:
2329:
2323:
2320:
1973:
1969:
1961:
1957:
1950:
1946:
1941:
1937:
1935:
1929:
1925:
1918:
1907:
1903:
1899:
1893:
1888:
1884:
1877:
1871:
1867:
1863:
1857:
1853:
1849:
1838:
1830:
1820:
1806:
954:
945:
936:
927:
880:
766:
749:
745:
743:
732:
724:
708:
704:
702:
693:
691:
682:
675:latus rectum
674:
672:
663:
661:
656:
652:
650:
643:
624:
616:
610:
603:
599:
588:
497:
494:
490:
483:
476:
469:
463:
462:(called the
451:eccentricity
449:
448:(called the
439:
438:(called the
425:
405:
398:
391:
387:eccentricity
364:
359:
355:
351:
344:closed curve
325:
318:
313:
305:
299:
287:
231:
126:eccentricity
124:
120:
114:
104:
63:
59:
55:
53:
10928:Polar curve
10008:Mineola, NY
10000:Korn, T. M.
9989:, p. 6
9912:, p. 5
9897:, pp.
9857:, pp.
9432:T. L. Heath
9236:Spain, B.,
9066:Kendig 2005
9024:Cohen, D.,
8547:(or 0), or
8446:degenerate,
7725:base points
7713:five points
6548:point conic
6534:Line conics
6362:perspective
6276:perspective
5277:Jan de Witt
5267:John Wallis
5219:Cyclopaedia
4585:eigenvalues
3552:determinant
2192:Hyperbola:
1942:equilateral
1938:rectangular
11143:Categories
10923:Dual curve
10551:Topics in
10090:Berger, M.
9934:Downs 2003
9922:Downs 2003
9910:Downs 2003
9766:, p.
9740:Artzy 2008
9728:Artzy 2008
9704:Boyer 2004
9689:Boyer 2004
9543:Heidelberg
9456:Boyer 2004
9376:Boyer 2004
9364:Boyer 2004
9352:Downs 2003
9329:: 295–348.
8988:References
8951:Boyer 2004
8675:classified
8612:(PDEs) of
8450:indefinite
7648:; and let
7551:degeneracy
7422:degenerate
7348:osculating
6765:, a point
6606:involutory
6552:line conic
6495:projective
6272:projective
5969:degenerate
5191:Abu al-Jud
5160: 350
5136: 190
5097: 212
5090:Archimedes
5080:generatrix
5072:Menaechmus
5055:turbulence
4969:Properties
4070:See also:
3536:Invariants
2762:degenerate
2327:-axis and
2127:Parabola:
746:minor axis
705:major axis
319:degenerate
296:Definition
86:, and the
11036:Morphisms
10784:Bitangent
10506:MathWorld
10380:, Dover,
10251:, Dover,
10179:, Dover,
10173:(2004) ,
10156:, Dover,
10152:(2008) ,
10014:, 1961),
9779:Eves 1963
9677:Katz 1998
9549:, 1983),
9517:, 1968),
9444:Eves 1963
9413:Eves 1963
9388:Katz 1998
9036:, 2006),
9001:Eves 1963
8798:
8748:
8699:
8688:≤
8636:include:
8565:−
8470:, zero –
8455:Curvature
8442:definite,
8413:−
8295:ℓ
8247:ℓ
8233:−
8230:⋯
8227:−
8203:−
8182:⋯
7981:μ
7961:λ
7922:μ
7906:λ
7877:μ
7871:λ
7833:μ
7817:λ
7717:collinear
7493:or to an
7445:empty set
7367:hyperbola
7275:−
6609:bijection
6478:π
6444:bijection
6372:π
6286:π
6156:in 1867.
6150:synthetic
6112:collinear
5538:notation
5319:astronomy
5312:Hyperbola
5287:kinematic
5164:directrix
4983:collinear
4893:θ
4890:
4841:increases
4807:λ
4797:λ
4790:Δ
4710:−
4695:λ
4677:−
4668:λ
4565:λ
4538:λ
4499:Δ
4490:λ
4475:−
4462:~
4441:Δ
4432:λ
4417:−
4404:~
4343:λ
4333:λ
4318:−
4305:~
4278:λ
4263:λ
4248:−
4235:~
4200:~
4185:~
4030:−
4018:Δ
3983:Δ
3977:−
3949:−
3933:Δ
3927:−
3886:Δ
3810:−
3781:η
3748:−
3490:hyperbola
3297:−
2638:ψ
2635:
2623:ψ
2620:
2611:±
2594:θ
2591:
2579:θ
2576:
2555:Hyperbola
2472:θ
2469:
2457:θ
2454:
2410:θ
2407:
2395:θ
2392:
2226:−
2044:Ellipse:
1843:. Define
1542:−
1507:hyperbola
1354:−
1263:−
1204:−
1096:∞
922:equation
781:ℓ
569:β
566:
558:α
555:
526:α
506:β
464:directrix
356:hyperbola
336:hyperbola
282:Hyperbola
121:directrix
80:hyperbola
10436:(1988),
10408:76087042
10310:(1998),
10268:(1963),
10216:(1964),
10196:Geometry
9843:Hartmann
9803:Hartmann
9742:, p. 159
9616:(2010).
9501:, &
9244:Pergamon
9030:Stamford
8947:Plutarch
8877:See also
7567:cylinder
7375:parabola
6809:and let
6663:Gergonne
6592:polarity
6581:polarity
6544:envelope
6364:mapping
6278:mapping
6274:but not
6073:midpoint
6045:Metrical
5308:Parabola
4963:dynamics
4583:are the
3472:parabola
3411:, then:
2495:Parabola
1982:Circle:
1813:rotation
1384:parabola
614:. (Here
352:parabola
348:parallel
332:parabola
275:Parabola
84:parabola
11096:Tacnode
11081:Crunode
9845:, p. 19
9817:, p. 65
9805:, p. 38
9662:10 June
9511:Hoboken
8464:surface
7645:
7623:
7615:
7601:
7371:ellipse
7344:tangent
7007:
6991:
6904:
6888:
6884:
6868:
6829:. Then
6538:By the
5372:quadric
5304:Ellipse
5202:Al-Kuhi
5195:quartic
5061:History
4938:0 <
3428:ellipse
3330:is the
2867:A, B, C
2748:In the
2433:Ellipse
1936:For a
1892:, with
1113:ellipse
737:, with
677:is the
468:0 <
466:). For
328:ellipse
278:
268:Ellipse
242:complex
88:ellipse
11076:Acnode
11000:Moduli
10470:
10452:
10422:
10406:
10384:
10364:
10344:
10334:Conics
10322:
10255:
10226:
10203:
10183:
10160:
10138:
10098:p. 127
10076:, pg.
10058:
9628:
9596:
9571:
9539:Berlin
9519:p. 219
9482:
9172:
9038:p. 844
8673:) are
7695:> 0
7681:< 0
7669:. If
7555:double
7398:circle
6923:, 0),
6837:meets
6757:, say
6604:is an
6104:circle
6071:, the
5536:matrix
5534:Or in
5323:orbits
5321:: the
5310:, and
5300:Circle
5222:, 1728
5208:Europe
5155:(died
5145:Conics
5131:(died
5121:Conics
5092:(died
5086:Euclid
5047:smooth
4956:> 1
4942:< 1
4914:where
4782:, and
4758:— and
4529:where
3870:η = −1
3860:where
3486:> 0
3452:circle
3424:< 0
3326:where
2752:, the
2371:Circle
1895:radius
964:circle
844:
811:
778:
657:center
486:> 1
472:< 1
340:circle
338:. The
334:, and
321:conics
314:nappes
261:Circle
92:circle
90:; the
82:, the
10293:(PDF)
10016:p. 42
9899:52–53
9859:48–49
9656:(PDF)
9649:(PDF)
9551:p. 73
9319:(PDF)
8924:Notes
8462:of a
8138:, as
8074:above
7434:point
7390:(1, –
6968:into
6949:and
6817:meet
6797:meet
6777:meet
6701:. An
6674:polar
6442:is a
6327:onto
6250:and
5399:In a
3862:η = 1
3576:trace
3574:(the
3269:below
2756:of a
2754:graph
679:chord
441:focus
428:locus
394:= 1/2
302:plane
116:focus
76:plane
68:curve
66:is a
62:or a
60:conic
11086:Cusp
10468:ISBN
10450:ISBN
10420:ISBN
10404:LCCN
10382:ISBN
10362:ISBN
10342:ISBN
10320:ISBN
10300:2014
10253:ISBN
10224:ISBN
10201:ISBN
10181:ISBN
10158:ISBN
10136:ISBN
10056:ISBN
9664:2011
9626:ISBN
9594:ISBN
9569:ISBN
9480:ISBN
9170:ISBN
8814:>
8715:<
8458:The
8081:oval
7973:and
7782:and
7430:apex
7394:, 0)
7388:and
7386:, 0)
7382:(1,
7158:and
7150:and
7126:(0,
7121:and
7108:1 ≤
7106:for
6958:, 0)
6911:ABCD
6707:line
6705:(or
6692:pole
6689:the
6683:and
6656:) =
6647:and
6642:) =
6468:axis
6095:and
6067:and
5257:and
5239:and
5008:≤5.
4556:and
3528:and
3520:and
3443:and
3324:− 4Δ
2865:and
2632:sinh
2617:cosh
2366:as,
2349:and
2170:>
1966:and
1921:, 0)
1841:, 0)
1833:, 0)
1815:and
1451:N/A
898:>
744:The
735:, 0)
729:and
727:, 0)
703:The
692:The
673:The
662:The
651:The
360:both
310:cone
238:real
9968:doi
8868:In
8782:or
8648:PSL
8281:so
7900:det
7688:= 0
7674:= 0
7667:≠ 0
7657:− 4
7627:BED
7595:= (
7069:to
7035:to
6943:, 2
6935:),
6931:, 2
6906:= 1
6825:at
6805:in
6785:in
6695:of
6677:of
6633:by
6298:of
6123:= 0
5420:In
5279:'s
5143:or
4949:= 1
4934:= 0
4887:cos
4845:In
4215:as
3545:– 4
3504:= 0
3495:if
3482:− 4
3477:if
3468:= 0
3464:− 4
3459:if
3448:= 0
3433:if
3420:− 4
3415:if
3271:).
2588:tan
2573:sec
2466:sin
2451:cos
2404:sin
2389:cos
2354:= −
1972:, −
1940:or
1928:= −
1882:so
1880:= 0
689:).
563:cos
552:cos
479:= 1
408:= 2
401:= 1
280:4:
273:3:
266:2:
259:1:
111:set
11145::
10503:.
10444:,
10402:,
10340:,
10336:,
10134:.
10130:.
10092:,
10078:64
10054:,
10052:63
10010::
10002:,
9964:22
9962:,
9768:72
9696:^
9624:.
9622:30
9545::
9533:,
9513::
9505:,
9474:.
9327:14
9325:.
9321:.
9300:.
9227:^
9187:^
9179:,
9032::
8795:tr
8745:tr
8696:tr
8662:SL
8279:m,
8271:k,
8090:.
7731:.
7697:.
7672:β
7659:AC
7653:=
7635:AE
7633:−
7631:CD
7629:−
7621:+
7599:−
7597:AC
7593:β
7537:0.
7404:.
7354:.
7330:CP
7324:.
7317:CP
7145:,
7112:≤
7099:DD
7096:∩
7090:AA
7056:AB
7022:BC
7014:BC
6984:AB
6976:AC
6964:BC
6954:(−
6939:(−
6886:+
6841:EG
6833:AN
6821:LM
6813:CD
6801:EG
6793:BC
6789:,
6781:DE
6773:AB
6761:EG
6748:,
6744:,
6740:,
6736:,
6716:.
6665:,
6594:,
6590:A
6493:A
6490:.
6360:A
6148:A
6114:.
6099:.
6089:AB
6077:AB
5996:,
5992:,
5988:,
5984:,
5980:,
5971:.
5744:.
5725:0.
5519:0.
5337:.
5306:,
5302:,
5204:.
5157:c.
5133:c.
5107:.
5094:c.
5057:.
5042:.
4989:.
3710:=
3708:AC
3593:+
3569:+
3562:/4
3558:–
3556:AC
3547:AC
3532:.
3500:+
3492:;
3484:AC
3466:AC
3438:=
3430:;
3422:AC
3253:0.
3055:0.
2661::
2557::
2497::
2435::
2373::
2359:.
2344:=
1978:.
1968:(−
1960:,
1949:=
1906:=
1902:=
1887:=
1870:+
1866:=
1856:−
1852:=
1837:(±
1829:(±
958:)
949:)
940:)
931:)
913:.
723:(−
597:.
330:,
292:.
217:0.
58:,
54:A
10544:e
10537:t
10530:v
10517:.
10509:.
10428:.
10144:.
10100:.
10080:.
10031:.
10018:.
10006:(
9977:.
9970::
9861:.
9666:.
9634:.
9602:.
9577:.
9553:.
9541:/
9537:(
9521:.
9509:(
9488:.
9246:.
9040:.
9028:(
8860:.
8820:,
8817:1
8811:2
8807:/
8802:|
8791:|
8770:,
8767:1
8764:=
8761:2
8757:/
8752:|
8741:|
8721:,
8718:1
8712:2
8708:/
8703:|
8692:|
8685:0
8670:)
8668:R
8666:(
8664:2
8656:)
8654:R
8652:(
8650:2
8603:.
8573:2
8569:y
8560:2
8556:x
8533:2
8529:x
8509:,
8504:2
8500:y
8496:+
8491:2
8487:x
8421:2
8417:y
8408:2
8404:x
8379:2
8375:x
8350:2
8346:y
8342:+
8337:2
8333:x
8310:.
8307:n
8304:=
8301:m
8298:+
8292:+
8289:k
8275:ℓ
8257:,
8252:2
8244:+
8241:k
8237:x
8222:2
8217:1
8214:+
8211:k
8207:x
8198:2
8193:k
8189:x
8185:+
8179:+
8174:2
8169:2
8165:x
8161:+
8156:2
8151:1
8147:x
8132:n
8039:0
8035:C
8009:0
8005:C
7941:0
7938:=
7935:)
7930:2
7926:C
7919:+
7914:1
7910:C
7903:(
7880:)
7874:,
7868:(
7846:.
7841:2
7837:C
7830:+
7825:1
7821:C
7795:2
7791:C
7768:1
7764:C
7693:α
7686:α
7679:α
7665:β
7655:B
7651:α
7642:4
7639:/
7619:F
7617:)
7612:4
7609:/
7605:B
7587:β
7534:=
7531:1
7528:+
7523:2
7519:y
7515:+
7510:2
7506:x
7481:,
7478:0
7475:=
7472:1
7469:+
7464:2
7460:x
7392:i
7384:i
7291:1
7288:=
7283:2
7279:w
7270:2
7266:x
7245:,
7242:w
7239:i
7236:=
7233:y
7213:1
7210:=
7205:2
7201:y
7197:+
7192:2
7188:x
7176:C
7160:D
7156:A
7152:P
7147:D
7143:A
7138:D
7134:A
7130:)
7128:b
7124:P
7119:A
7114:n
7110:i
7103:i
7094:i
7084:B
7080:A
7075:n
7072:D
7066:1
7063:D
7050:C
7046:B
7041:n
7038:A
7032:1
7029:A
7003:a
6999:/
6995:b
6970:n
6956:a
6952:D
6947:)
6945:b
6941:a
6937:C
6933:b
6929:a
6927:(
6925:B
6921:a
6919:(
6917:A
6900:b
6896:/
6892:y
6880:a
6876:/
6872:x
6851:E
6847:F
6827:N
6807:M
6787:L
6767:F
6755:E
6750:E
6746:D
6742:C
6738:B
6734:A
6698:q
6686:Q
6680:Q
6668:q
6658:Q
6654:q
6652:(
6650:π
6644:q
6640:Q
6638:(
6636:π
6630:q
6624:Q
6614:P
6601:P
6596:π
6518:V
6515:,
6512:U
6454:a
6430:)
6427:V
6424:(
6421:B
6401:)
6398:U
6395:(
6392:B
6344:)
6341:V
6338:(
6335:B
6315:)
6312:U
6309:(
6306:B
6258:V
6238:U
6218:V
6215:,
6212:U
6192:)
6189:V
6186:(
6183:B
6180:,
6177:)
6174:U
6171:(
6168:B
6121:e
6097:B
6093:A
6081:C
6069:B
6065:A
6025:.
6020:5
6015:P
6000:)
5998:F
5994:E
5990:D
5986:C
5982:B
5978:A
5976:(
5949:,
5945:)
5938:F
5933:E
5928:D
5921:E
5916:C
5911:B
5904:D
5899:B
5894:A
5887:(
5883:=
5880:M
5854:,
5851:0
5848:=
5843:2
5839:z
5835:F
5832:+
5829:z
5826:y
5823:E
5820:2
5817:+
5814:z
5811:x
5808:D
5805:2
5802:+
5797:2
5793:y
5789:C
5786:+
5783:y
5780:x
5777:B
5774:2
5771:+
5766:2
5762:x
5758:A
5722:=
5718:)
5711:z
5704:y
5697:x
5690:(
5685:)
5678:F
5673:2
5669:/
5665:E
5660:2
5656:/
5652:D
5645:2
5641:/
5637:E
5632:C
5627:2
5623:/
5619:B
5612:2
5608:/
5604:D
5599:2
5595:/
5591:B
5586:A
5579:(
5574:)
5567:z
5562:y
5557:x
5550:(
5516:=
5511:2
5507:z
5503:F
5500:+
5497:z
5494:y
5491:E
5488:+
5485:z
5482:x
5479:D
5476:+
5471:2
5467:y
5463:C
5460:+
5457:y
5454:x
5451:B
5448:+
5443:2
5439:x
5435:A
5380:R
5314:.
5006:k
5002:k
4998:k
4954:e
4947:e
4940:e
4932:e
4923:l
4917:e
4899:,
4884:e
4881:+
4878:1
4874:l
4869:=
4866:r
4852:x
4839:e
4811:2
4801:1
4793:=
4766:S
4743:0
4740:=
4737:)
4732:2
4728:)
4724:2
4720:/
4716:B
4713:(
4707:C
4704:A
4701:(
4698:+
4692:)
4689:C
4686:+
4683:A
4680:(
4672:2
4643:)
4636:C
4631:2
4627:/
4623:B
4616:2
4612:/
4608:B
4603:A
4596:(
4569:2
4542:1
4514:,
4511:1
4508:=
4502:)
4494:2
4486:(
4482:/
4478:S
4469:2
4459:y
4450:+
4444:)
4436:1
4428:(
4424:/
4420:S
4411:2
4401:x
4369:,
4366:1
4363:=
4357:)
4352:2
4347:2
4337:1
4329:(
4325:/
4321:S
4312:2
4302:y
4293:+
4287:)
4282:2
4272:2
4267:1
4259:(
4255:/
4251:S
4242:2
4232:x
4197:y
4191:,
4182:x
4155:0
4152:=
4149:F
4146:+
4143:y
4140:E
4137:+
4134:x
4131:D
4128:+
4123:2
4119:y
4115:C
4112:+
4109:y
4106:x
4103:B
4100:+
4095:2
4091:x
4087:A
4050:.
4045:4
4040:2
4036:B
4027:C
4024:A
4021:=
3995:,
3992:0
3989:=
3986:]
3980:4
3972:2
3968:)
3964:C
3961:+
3958:A
3955:(
3952:[
3944:2
3940:e
3936:]
3930:4
3922:2
3918:)
3914:C
3911:+
3908:A
3905:(
3902:[
3899:+
3894:4
3890:e
3845:,
3834:2
3830:B
3826:+
3821:2
3817:)
3813:C
3807:A
3804:(
3799:+
3796:)
3793:C
3790:+
3787:A
3784:(
3772:2
3768:B
3764:+
3759:2
3755:)
3751:C
3745:A
3742:(
3737:2
3730:=
3727:e
3712:B
3706:4
3688:,
3685:0
3682:=
3679:F
3676:+
3673:y
3670:E
3667:+
3664:x
3661:D
3658:+
3653:2
3649:y
3645:C
3642:+
3639:y
3636:x
3633:B
3630:+
3625:2
3621:x
3617:A
3595:E
3591:D
3585:F
3571:C
3567:A
3560:B
3543:B
3530:B
3526:A
3522:B
3518:A
3510:.
3502:C
3498:A
3480:B
3474:;
3462:B
3446:B
3440:C
3436:A
3418:B
3393:.
3389:|
3382:C
3377:2
3373:/
3369:B
3362:2
3358:/
3354:B
3349:A
3342:|
3328:Δ
3306:C
3303:A
3300:4
3292:2
3288:B
3250:=
3245:)
3239:1
3232:y
3225:x
3219:(
3212:)
3206:F
3201:2
3197:/
3193:E
3188:2
3184:/
3180:D
3173:2
3169:/
3165:E
3160:C
3155:2
3151:/
3147:B
3140:2
3136:/
3132:D
3127:2
3123:/
3119:B
3114:A
3108:(
3101:)
3095:1
3090:y
3085:x
3079:(
3052:=
3049:F
3046:+
3041:)
3035:y
3028:x
3022:(
3015:)
3009:E
3004:D
2998:(
2993:+
2988:)
2982:y
2975:x
2969:(
2962:)
2956:C
2951:2
2947:/
2943:B
2936:2
2932:/
2928:B
2923:A
2917:(
2910:)
2904:y
2899:x
2893:(
2846:,
2843:0
2840:=
2837:F
2834:+
2831:y
2828:E
2825:+
2822:x
2819:D
2816:+
2811:2
2807:y
2803:C
2800:+
2797:y
2794:x
2791:B
2788:+
2783:2
2779:x
2775:A
2726:.
2720:2
2716:c
2711:=
2708:d
2700:,
2696:)
2690:t
2687:d
2682:,
2679:t
2676:d
2672:(
2653:,
2641:)
2629:b
2626:,
2614:a
2608:(
2600:,
2597:)
2585:b
2582:,
2570:a
2567:(
2538:,
2535:)
2532:t
2529:a
2526:2
2523:,
2518:2
2514:t
2510:a
2507:(
2478:,
2475:)
2463:b
2460:,
2448:a
2445:(
2416:,
2413:)
2401:a
2398:,
2386:a
2383:(
2356:x
2352:y
2346:x
2342:y
2336:x
2330:y
2324:x
2304:.
2299:2
2295:c
2291:=
2288:y
2285:x
2259:,
2256:1
2253:=
2246:2
2242:b
2236:2
2232:y
2219:2
2215:a
2209:2
2205:x
2176:,
2173:0
2167:a
2159:,
2156:x
2153:a
2150:4
2147:=
2142:2
2138:y
2111:,
2108:1
2105:=
2098:2
2094:b
2088:2
2084:y
2078:+
2071:2
2067:a
2061:2
2057:x
2028:,
2023:2
2019:a
2015:=
2010:2
2006:y
2002:+
1997:2
1993:x
1976:)
1974:c
1970:c
1964:)
1962:c
1958:c
1956:(
1951:y
1947:x
1930:a
1926:x
1919:a
1917:(
1913:x
1908:b
1904:a
1900:r
1889:b
1885:a
1878:c
1872:b
1868:a
1864:c
1858:b
1854:a
1850:c
1845:b
1839:c
1831:a
1825:x
1756:2
1752:b
1748:+
1743:2
1739:a
1732:2
1728:b
1702:a
1697:2
1693:b
1665:2
1661:b
1657:+
1652:2
1648:a
1618:2
1614:a
1608:2
1604:b
1598:+
1595:1
1572:1
1569:=
1562:2
1558:b
1552:2
1548:y
1535:2
1531:a
1525:2
1521:x
1489:a
1486:2
1464:a
1461:2
1436:1
1414:x
1411:a
1408:4
1405:=
1400:2
1396:y
1362:2
1358:b
1349:2
1345:a
1338:2
1334:b
1308:a
1303:2
1299:b
1271:2
1267:b
1258:2
1254:a
1224:2
1220:a
1214:2
1210:b
1201:1
1178:1
1175:=
1168:2
1164:b
1158:2
1154:y
1148:+
1141:2
1137:a
1131:2
1127:x
1074:a
1052:0
1030:0
1006:2
1002:a
998:=
993:2
989:y
985:+
980:2
976:x
955:p
946:ℓ
937:c
928:e
901:0
895:b
892:,
889:a
864:e
861:a
856:=
853:c
850:+
847:p
823:e
820:a
817:=
814:c
790:e
787:p
784:=
762:b
758:b
754:b
752:(
739:a
733:a
731:(
725:a
719:x
715:a
713:(
698:p
696:(
687:ℓ
685:(
668:c
666:(
646:e
625:a
623:2
617:a
611:a
609:2
604:a
602:2
575:.
529:,
484:e
477:e
470:e
460:L
456:P
446:e
436:F
432:P
420:∞
412:0
406:e
399:e
392:e
214:=
211:F
208:+
205:y
202:E
199:+
196:x
193:D
190:+
185:2
181:y
177:C
174:+
171:y
168:x
165:B
162:+
157:2
153:x
149:A
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.