360:
388:
411:" by Dyn, Levin and Gregory (1990), who extended the four-point interpolatory subdivision scheme for curves to a subdivision scheme for surface. Zorin, Schröder and Sweldens (1996) noticed that the butterfly scheme cannot generate smooth surfaces for irregular triangle meshes and thus modified this scheme. Kobbelt (1996) further generalized the four-point interpolatory subdivision scheme for curves to the tensor product subdivision scheme for surfaces. In 1991, Nasri proposed a scheme for interpolating Doo-Sabin; while in 1993 Halstead, Kass, and DeRose proposed one for Catmull-Clark.
103:
374:
111:
130:
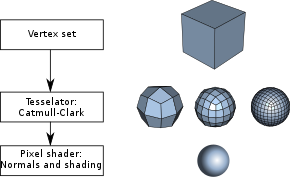
is then applied to this mesh. This process takes that mesh and subdivides it, creating new vertices and new faces. The positions of the new vertices in the mesh are computed based on the positions of nearby old vertices, edges, and/or faces. In many refinement schemes, the positions of old vertices
138:
mesh than the original one, containing more polygonal faces (often by a factor of 4). This resulting mesh can be passed through the same refinement scheme again and again to produce more and more refined meshes. Each iteration is often called a subdivision
86:
into smaller faces that better approximate the final underlying curved surface. Less commonly, a simple algorithm is used to add geometry to a mesh by subdividing the faces into smaller ones without changing the overall shape or volume.
319:(1997–1999) – The mid-edge subdivision scheme was proposed independently by Peters-Reif (1997) and Habib-Warren (1999). The former used the mid-point of each edge to build the new mesh. The latter used a four-directional
281:(1978), Quads – The second subdivision scheme was developed by Doo and Sabin, who successfully extended Chaikin's corner-cutting method (George Chaikin, 1974) for curves to surfaces. They used the analytical expression of
249:
means that the limit surfaces approximate the initial meshes, and that after subdivision the newly generated control points are not in the limit surfaces. There are five approximating subdivision schemes:
327:
continuous limit surfaces on initial meshes with arbitrary topology. (Mid-Edge subdivision, which could be called "√2 subdivision" since two steps halve distances, could be considered the slowest.)
150:
subdivision surface is the surface produced from this process being iteratively applied infinitely many times. In practical use however, this algorithm is only applied a limited, and fairly small (
238:
Subdivision surface schemes can also be categorized by the type of polygon that they operate on: some function best for quadrilaterals (quads), while others primarily operate on triangles (tris).
725:
Jos Stam, "Exact
Evaluation of Catmull-Clark Subdivision Surfaces at Arbitrary Parameter Values", Proceedings of SIGGRAPH'98. In Computer Graphics Proceedings, ACM SIGGRAPH, 1998, 395–404
415:
681:
Halstead, M., Kass, M., and DeRose, T. Efficient, Fair
Interpolation Using Catmull-Clark Surfaces. In Computer Graphics Proceedings (1993), Annual Conference Series, ACM Siggraph
289:
limit surfaces with arbitrary topology for arbitrary initial meshes. An auxiliary point can improve the shape of Doo-Sabin subdivision. After a subdivision, all vertices have
316:
407:
After subdivision, the control points of the original mesh and the newly generated control points are interpolated on the limit surface. The earliest work was so-called "
330:
171:
408:
91:
333:(2000), Triangles – This scheme was developed by Kobbelt and offers several interesting features: it handles arbitrary triangular meshes, it is
456:
223:
In general, approximating schemes have greater smoothness, but the user has less overall control of the outcome. This is analogous to
427:
421:
672:
Nasri, A. H. Surface interpolation on irregular networks with normal conditions. Computer Aided
Geometric Design 8 (1991), 89–96.
746:
804:
505:
52:
341:
continuous and it offers a natural adaptive refinement when required. It exhibits at least two specificities: it is a
445:
365:
254:
115:
466:
contributed a method for exact evaluation for
Catmull-Clark subdivision surfaces under arbitrary parameter values.
449:
799:
484:
379:
278:
177:
261:
430:(1996), Quads – a variational subdivision method that tries to overcome uniform subdivision drawbacks
193:
393:
298:
216:
Interpolating schemes are required to match the original position of vertices in the original mesh.
712:
Ulrich Reif. 1995. A unified approach to subdivision algorithms near extraordinary vertices.
600:
359:
387:
639:
338:
334:
324:
310:
306:
291:
286:
272:
268:
185:
778:
267:
knot insertion. For arbitrary initial meshes, this scheme generates limit surfaces that are
153:
224:
189:
36:
481:(1997) – a Pixar movie which pioneered use of subdivision surfaces to represent human skin
8:
76:
529:
784:
752:
700:
Department of
Computer Science, California Institute of Technology, Pasadena, CA 91125
204:
Subdivision surface refinement schemes can be broadly classified into two categories:
309:
continuous limit surfaces everywhere except at extraordinary vertices where they are
785:
Surface
Subdivision Methods in CGAL, the Computational Geometry Algorithms Library
692:
645:
772:
219:
Approximating schemes are not; they can and will adjust these positions as needed.
373:
102:
83:
345:
scheme for triangle meshes and it has a slower refinement rate than primal ones.
228:
545:
477:
424:(1996), Quads – designed to overcome artifacts generated by irregular topology
793:
762:
441:
301:(1987), Triangles – Loop proposed his subdivision scheme based on a quartic
285:
uniform B-spline surface to generate their subdivision procedure to produce
661:
625:
56:
660:, 27th annual conference on Computer graphics and interactive techniques,
570:
282:
775:, Ulrich Reif (Computer Aided Geometric Design 12(2):153–174 March 1995)
773:
A unified approach to subdivision algorithms near extraordinary vertices
588:
320:
302:
110:
271:
continuous everywhere except at extraordinary vertices where they are
123:
80:
60:
131:
are also altered (possibly based on the positions of new vertices).
766:
756:
463:
337:
continuous everywhere except at extraordinary vertices where it is
264:
258:
232:
738:
126:
in nature. The process starts with a base level polygonal mesh. A
487:(NURBS) surfaces – another method of representing curved surfaces
459:
solved subdivision surface behaviour near extraordinary vertices.
781:, software to perform subdivision using the most popular schemes
624:, ACM Transactions on Graphics 16(4) (October 1997) p.420-431,
20:
693:"Interpolating Subdivision for Meshes with Arbitrary Topology"
644:, Computer Aided Geometric Design 16(4) (May 1999) p.223-247,
745:
completed in 1997 that introduced subdivision surfaces using
742:
27:
544:, Springer series Geometry and Computing monograph 3, 2008,
188:
node for quad refined meshes) of a subdivision surface is a
26:"SubD" redirects here. For the subminiature connector, see
231:
are required to interpolate certain control points, while
622:
The simplest subdivision scheme for smoothing polyhedra
558:
Analysis of generalized B-spline subdivision algorithms
305:
of six direction vectors to provide a rule to generate
67:, can be calculated from the coarse mesh, known as the
63:
algorithmic method. The curved surface, the underlying
19:"Subdiv" redirects here. For submarine divisions, see
691:
Zorin, Denis; Schröder, Peter; Sweldens, Wim (1996).
690:
156:
143:, starting at zero (before any refinement occurs).
585:Point-augmented biquadratic C subdivision surfaces
418:(1990), Triangles – named after the scheme's shape
165:
16:Curved curface derived from a coarse polygon mesh
791:
560:, SIAM J of Numer. Anal. 32 (2) 1998, p.728-748
55:represented by the specification of a coarser
550:
440:1978: Subdivision surfaces were described by
779:Subdivision of Surface and Volumetric Meshes
79:of an iterative process of subdividing each
530:Blender: Reduce Polygons – Simply Explained
448:), and by Daniel Doo and Malcom Sabin (see
323:to build the scheme. This scheme generates
577:
638:Edge and vertex insertion for a class of
534:
598:
402:
241:
109:
101:
650:
792:
763:Subdivision for Modeling and Animation
753:Subdivision for Modeling and Animation
614:
199:
90:The opposite is reducing polygons or
719:
706:
630:
235:are not (and are more approximate).
106:Simple subdivision of a cube up to 3
741: : Oscar winning animation by
434:
122:A subdivision surface algorithm is
118:pipeline using a subdivision method
13:
275:continuous (Peters and Reif 1998).
14:
816:
732:
446:Catmull-Clark subdivision surface
608:On-Line Geometric Modeling Notes
587:, Graphical Models, 77, p.18-26
386:
372:
358:
714:Computer Aided Geometric Design
684:
675:
666:
592:
583:K. Karciauskas and J. Peters:
571:"Chaikin Curves in Processing"
563:
523:
498:
450:Doo-Sabin subdivision surfaces
1:
749:(along with cloth simulation)
491:
485:Non-uniform rational B-spline
257:(1978), Quads – generalizes
7:
470:
317:Mid-Edge subdivision scheme
227:surfaces and curves, where
97:
10:
821:
805:Multivariate interpolation
25:
18:
747:Catmull-Clark subdivision
636:A. Habib and J. Warren:
313:continuous (Zorin 1997).
134:This process produces a
620:J. Peters and U. Reif:
556:J. Peters and U. Reif:
540:J. Peters and U. Reif:
43:(commonly shortened to
599:Joy, Ken (1996–2000).
506:"Subdivision Surfaces"
192:with a parametrically
167:
166:{\displaystyle \leq 5}
119:
107:
610:– via UC Davis.
403:Interpolating schemes
331:√3 subdivision scheme
242:Approximating schemes
168:
113:
105:
800:3D computer graphics
642:subdivision surfaces
601:"DOO-SABIN SURFACES"
542:Subdivision Surfaces
182:extraordinary vertex
176:Mathematically, the
173:), number of times.
154:
75:, as the functional
37:3D computer graphics
444:and Jim Clark (see
352:Subdivision Schemes
41:subdivision surface
422:Modified Butterfly
200:Refinement schemes
163:
120:
108:
59:and produced by a
769:2000 course notes
759:1999 course notes
255:Catmull and Clark
128:refinement scheme
812:
726:
723:
717:
710:
704:
703:
697:
688:
682:
679:
673:
670:
664:
654:
648:
634:
628:
618:
612:
611:
605:
596:
590:
581:
575:
574:
567:
561:
554:
548:
538:
532:
527:
521:
520:
518:
516:
502:
435:Key developments
409:butterfly scheme
390:
376:
362:
172:
170:
169:
164:
35:In the field of
820:
819:
815:
814:
813:
811:
810:
809:
790:
789:
735:
730:
729:
724:
720:
711:
707:
695:
689:
685:
680:
676:
671:
667:
655:
651:
635:
631:
619:
615:
603:
597:
593:
582:
578:
569:
568:
564:
555:
551:
539:
535:
528:
524:
514:
512:
510:nevercenter.com
504:
503:
499:
494:
473:
437:
405:
400:
399:
398:
397:
396:
391:
383:
382:
377:
369:
368:
363:
354:
353:
244:
202:
155:
152:
151:
100:
31:
24:
17:
12:
11:
5:
818:
808:
807:
802:
788:
787:
782:
776:
770:
760:
750:
734:
733:External links
731:
728:
727:
718:
716:. 12(2)153–174
705:
683:
674:
665:
658:√3-subdivision
649:
629:
613:
591:
576:
562:
549:
533:
522:
496:
495:
493:
490:
489:
488:
482:
472:
469:
468:
467:
460:
453:
436:
433:
432:
431:
425:
419:
404:
401:
392:
385:
384:
378:
371:
370:
364:
357:
356:
355:
351:
350:
349:
348:
347:
346:
328:
314:
296:
276:
243:
240:
221:
220:
217:
201:
198:
194:singular point
162:
159:
99:
96:
92:un-subdividing
51:) is a curved
15:
9:
6:
4:
3:
2:
817:
806:
803:
801:
798:
797:
795:
786:
783:
780:
777:
774:
771:
768:
764:
761:
758:
754:
751:
748:
744:
740:
737:
736:
722:
715:
709:
701:
694:
687:
678:
669:
663:
659:
653:
647:
643:
641:
633:
627:
623:
617:
609:
602:
595:
589:
586:
580:
572:
566:
559:
553:
547:
543:
537:
531:
526:
511:
507:
501:
497:
486:
483:
480:
479:
475:
474:
465:
461:
458:
454:
451:
447:
443:
442:Edwin Catmull
439:
438:
429:
426:
423:
420:
417:
414:
413:
412:
410:
395:
389:
381:
375:
367:
366:Catmull–Clark
361:
344:
340:
336:
332:
329:
326:
322:
318:
315:
312:
308:
304:
300:
297:
294:
293:
288:
284:
280:
277:
274:
270:
266:
263:
260:
256:
253:
252:
251:
248:
247:Approximating
239:
236:
234:
230:
229:Bézier curves
226:
218:
215:
214:
213:
211:
210:approximating
207:
206:interpolating
197:
195:
191:
187:
183:
179:
174:
160:
157:
149:
144:
142:
137:
132:
129:
125:
117:
112:
104:
95:
93:
88:
85:
82:
78:
74:
70:
66:
62:
58:
54:
50:
46:
42:
38:
33:
29:
22:
721:
713:
708:
699:
686:
677:
668:
657:
656:L. Kobbelt:
652:
637:
632:
621:
616:
607:
594:
584:
579:
565:
557:
552:
541:
536:
525:
513:. Retrieved
509:
500:
476:
406:
342:
290:
283:bi-quadratic
246:
245:
237:
222:
209:
205:
203:
181:
178:neighborhood
175:
147:
145:
140:
135:
133:
127:
121:
116:tessellation
89:
72:
69:control cage
68:
64:
57:polygon mesh
48:
45:SubD surface
44:
40:
34:
32:
739:Geri's Game
478:Geri's Game
457:Ulrich Reif
794:Categories
765:tutorial,
755:tutorial,
515:19 January
492:References
321:box spline
303:box-spline
73:outer mesh
65:inner mesh
416:Butterfly
380:Doo–Sabin
279:Doo-Sabin
233:B-Splines
158:≤
124:recursive
81:polygonal
61:recursive
767:SIGGRAPH
757:SIGGRAPH
471:See also
464:Jos Stam
265:B-spline
259:bi-cubic
98:Overview
428:Kobbelt
292:valence
262:uniform
184:(non-4-
53:surface
49:Subsurf
462:1998:
455:1995:
225:spline
190:spline
186:valent
180:of an
136:denser
21:SUBDIV
743:Pixar
696:(PDF)
604:(PDF)
148:limit
141:level
77:limit
28:D-Sub
517:2021
394:Loop
343:Dual
299:Loop
208:and
146:The
84:face
39:, a
662:doi
646:doi
626:doi
546:doi
71:or
47:or
796::
698:.
606:.
508:.
452:).
295:4.
212:.
196:.
114:A
94:.
702:.
640:C
573:.
519:.
339:C
335:C
325:C
311:C
307:C
287:C
273:C
269:C
161:5
30:.
23:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.