17:
62:
71:
626:) can be tessellated by 240 (2,4,5) triangles. The actions that transport one of these triangles to another give the full group of automorphisms of the surface (including reflections). Discounting reflections, we get the 120 automorphisms mentioned in the introduction. Note that 120 is less than 252, the maximum number of orientation preserving automorphisms allowed for a genus 4 surface, by
1285:
this hypothesis, particularly in the case of the Bolza surface, although providing a rigorous proof is still an open problem. Following this pattern, one may reasonably conjecture that Bring's surface maximizes the first positive eigenvalue of the
Laplacian (among surfaces in its topological class).
1284:
and Klein quartic have the largest symmetry groups among compact
Riemann surfaces of constant negative curvature in genera 2 and 3 respectively, and thus it has been conjectured that they maximize the first positive eigenvalue in the Laplace spectrum. There is strong numerical evidence to support
1169:, Bring's surface does not maximize the systole length among compact Riemann surfaces in its topological category (that is, surfaces having the same genus) despite maximizing the size of the automorphism group. The systole is presumably maximized by the surface referred to a M4 in (
1160:
821:
330:
1263:
1048:
581:
462:
1066:
147:
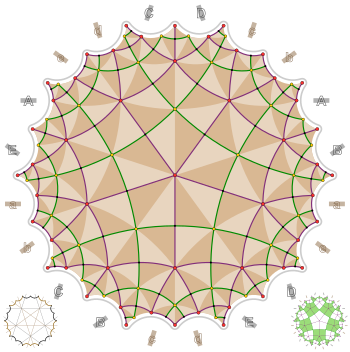
643:
1424:
403:
500:
620:
905:
885:
865:
845:
155:
1179:
915:. In particular, the group has four 1 dimensional, four 4 dimensional, four 5 dimensional, and two 6 dimensional irreducible representations, and we have
1165:
and multiplicity 20, a geodesic loop of that length consisting of the concatenated altitudes of twelve of the 240 (2,4,5) triangles. Similarly to the
1527:
921:
1950:
2042:
1679:
1639:
1520:
1406:
2119:
1730:
1629:
2109:
627:
1808:
1513:
544:
1155:{\displaystyle 12\sinh ^{-1}\left({\tfrac {1}{2}}{\sqrt {{\tfrac {1}{2}}({\sqrt {5}}-1)}}\right)\approx 4.60318}
408:
1955:
1876:
1866:
1803:
33:
1553:
912:
114:
1773:
1669:
538:
80:
2032:
1996:
1695:
1608:
2006:
1644:
816:{\displaystyle \langle r,\,s,\,t\,|\,r^{5}=s^{2}=t^{2}=rtrt=stst=(rs)^{4}=(sr^{3}sr^{2})^{2}=e\rangle }
123:
2144:
2052:
41:
37:
1965:
1945:
1881:
1798:
1700:
1659:
526:
of the 5 coordinates. This is the largest possible automorphism group of a genus 4 complex curve.
360:
1856:
1664:
1649:
887:
is a rotation of order 2 at the vertex where 4 (2,4,5) triangles meet in the tessellation, and
1763:
467:
2027:
1725:
1674:
1563:
1309:
908:
541:. It has genus 4. The full group of symmetries (including reflections) is the direct product
45:
602:
2114:
1975:
1634:
1453:
1416:
1384:
623:
519:
1886:
8:
1940:
1818:
1783:
1740:
1720:
596:
340:
21:
591:
Bring's curve can be obtained as a
Riemann surface by associating sides of a hyperbolic
325:{\displaystyle v+w+x+y+z=v^{2}+w^{2}+x^{2}+y^{2}+z^{2}=v^{3}+w^{3}+x^{3}+y^{3}+z^{3}=0.}
2081:
1861:
1841:
1654:
1398:
1258:{\displaystyle 2\cosh ^{-1}\left({\tfrac {1}{2}}(5+3{\sqrt {3}})\right)\approx 4.6245,}
890:
870:
850:
830:
599:). The identification pattern is given in the adjoining diagram. The icosagon (of area
505:
344:
84:
29:
1813:
1329:
Weber, Matthias (2005). "Kepler's small stellated dodecahedron as a
Riemann surface".
1970:
1917:
1788:
1603:
1598:
1402:
1392:
1372:
1057:
907:
is reflection in the real line. From this presentation, information about the linear
1280:
of Bring's surface, however, it could potentially be of interest in this field. The
1960:
1823:
1493:
1469:
1439:
1364:
1304:
118:
343:
who studied a similar construction in 1786 in a
Promotionschrift submitted to the
2086:
1891:
1833:
1735:
1558:
1537:
1460:
Schmutz, P. (1993), "Riemann surfaces with shortest geodesic of maximal length",
1449:
1412:
1380:
1277:
631:
534:
509:
16:
2060:
1758:
1583:
1568:
1545:
1368:
530:
61:
634:. This also tells us that there does not exist a Hurwitz surface of genus 4.
2138:
2101:
1871:
1851:
1778:
1573:
1505:
1498:
1444:
1394:
Lectures on the icosahedron and the solution of equations of the fifth degree
1376:
1348:
Meletemata quædam mathematica circa transformationem æquationem algebraicarum
1299:
1294:
1281:
1166:
355:
106:
2037:
2011:
2001:
1991:
1793:
1613:
1481:
1335:
1912:
1750:
523:
94:
1907:
1473:
867:
is a rotation of order 5 about the centre of the fundamental polygon,
1768:
70:
1043:{\displaystyle 4(1^{2})+4(4^{2})+4(5^{2})+2(6^{2})=4+64+100+72=240}
592:
25:
2091:
2076:
2071:
911:
of the symmetry group of Bring's surface can be computed using
637:
The full group of symmetries has the following presentation:
1482:"Kepler's small stellated dodecahedron as a Riemann surface"
1208:
1109:
1095:
1346:
Bring, Erland Samuel; Sommelius, Sven Gustaf (1786),
1182:
1069:
924:
893:
873:
853:
833:
646:
605:
547:
470:
411:
363:
158:
126:
51:
20-gon edges marked with the same letter are equal.
1257:
1154:
1042:
899:
879:
859:
839:
815:
614:
575:
494:
456:
397:
324:
141:
586:
2136:
533:of the sphere branched in 12 points, and is the
1535:
1422:
1345:
1521:
810:
647:
576:{\displaystyle S_{5}\times \mathbb {Z} _{2}}
1528:
1514:
1357:Journal of the London Mathematical Society
457:{\displaystyle \sum _{i=1}^{5}x_{i}^{k}=0}
24:for Bring's curve is a regular hyperbolic
1497:
1443:
673:
667:
663:
656:
563:
129:
15:
1459:
1170:
2137:
1951:Clifford's theorem on special divisors
1425:"The period matrices of Bring's curve"
1350:, Promotionschrift, University of Lund
630:. Therefore, Bring's surface is not a
1509:
1479:
1390:
1355:Edge, W. L. (1978), "Bring's curve",
1328:
336:
149:cut out by the homogeneous equations
1397:, Dover Phoenix Editions, New York:
1354:
13:
2120:Vector bundles on algebraic curves
2043:Weber's theorem (Algebraic curves)
1640:Hasse's theorem on elliptic curves
1630:Counting points on elliptic curves
1333:. Vol. 220. pp. 167–182.
1271:
14:
2156:
1423:Riera, G.; Rodriguez, R. (1992),
142:{\displaystyle \mathbb {P} ^{4}}
79:Bring's curve is related to the
69:
60:
1731:Hurwitz's automorphisms theorem
1173:). The systole length of M4 is
529:The curve can be realized as a
1956:Gonality of an algebraic curve
1867:Differential of the first kind
1322:
1238:
1219:
1136:
1120:
1007:
994:
985:
972:
963:
950:
941:
928:
795:
765:
753:
743:
669:
628:Hurwitz's automorphism theorem
587:Fundamental domain and systole
405:satisfies Bring's curve since
1:
2110:Birkhoff–Grothendieck theorem
1809:Nagata's conjecture on curves
1680:Schoof–Elkies–Atkin algorithm
1554:Five points determine a conic
1315:
1670:Supersingular elliptic curve
539:small stellated dodecahedron
398:{\displaystyle x^{5}+ax+b=0}
81:small stellated dodecahedron
7:
1877:Riemann's existence theorem
1804:Hilbert's sixteenth problem
1696:Elliptic curve cryptography
1609:Fundamental pair of periods
1288:
10:
2161:
2007:Moduli of algebraic curves
1276:Little is known about the
1060:of the surface has length
28:(20-gon), shown here with
2100:
2051:
2020:
1984:
1933:
1926:
1900:
1832:
1749:
1713:
1688:
1622:
1591:
1582:
1544:
1268:and has multiplicity 36.
105:and, by analogy with the
42:order-4 pentagonal tiling
1774:Cayley–Bacharach theorem
1701:Elliptic curve primality
1499:10.2140/pjm.2005.220.167
1480:Weber, Matthias (2005),
1445:10.2140/pjm.1992.154.179
1369:10.1112/jlms/s2-18.3.539
847:is the identity action,
495:{\displaystyle k=1,2,3.}
2033:Riemann–Hurwitz formula
1997:Gromov–Witten invariant
1857:Compact Riemann surface
1645:Mazur's torsion theorem
583:, which has order 240.
1650:Modular elliptic curve
1391:Klein, Felix (2003) ,
1259:
1156:
1044:
901:
881:
861:
841:
817:
616:
615:{\displaystyle 12\pi }
577:
496:
458:
432:
399:
347:. Note that the roots
326:
143:
53:
1564:Rational normal curve
1310:First Hurwitz triplet
1260:
1157:
1045:
909:representation theory
902:
882:
862:
842:
818:
617:
578:
497:
459:
412:
400:
327:
144:
19:
2115:Stable vector bundle
1976:Weil reciprocity law
1966:Riemann–Roch theorem
1946:Brill–Noether theory
1882:Riemann–Roch theorem
1799:Genus–degree formula
1660:Mordell–Weil theorem
1635:Division polynomials
1180:
1067:
922:
891:
871:
851:
831:
644:
624:Gauss-Bonnet theorem
603:
545:
508:of the curve is the
468:
409:
361:
156:
124:
1927:Structure of curves
1819:Quartic plane curve
1741:Hyperelliptic curve
1721:De Franchis theorem
1665:Nagell–Lutz theorem
597:fundamental polygon
447:
341:Erland Samuel Bring
36:in violet. It is a
32:graph in green and
22:fundamental polygon
1934:Divisors on curves
1726:Faltings's theorem
1675:Schoof's algorithm
1655:Modularity theorem
1474:10.1007/BF01896258
1399:Dover Publications
1255:
1217:
1152:
1118:
1104:
1040:
897:
877:
857:
837:
813:
612:
573:
537:associated to the
506:automorphism group
492:
454:
433:
395:
345:University of Lund
322:
139:
85:dodecadodecahedron
54:
30:dodecadodecahedral
2132:
2131:
2128:
2127:
2028:Hasse–Witt matrix
1971:Weierstrass point
1918:Smooth completion
1887:Teichmüller space
1789:Cubic plane curve
1709:
1708:
1623:Arithmetic theory
1604:Elliptic integral
1599:Elliptic function
1408:978-0-486-49528-6
1236:
1216:
1139:
1128:
1117:
1103:
900:{\displaystyle t}
880:{\displaystyle s}
860:{\displaystyle r}
840:{\displaystyle e}
52:
2152:
2145:Algebraic curves
1961:Jacobian variety
1931:
1930:
1834:Riemann surfaces
1824:Real plane curve
1784:Cramer's paradox
1764:Bézout's theorem
1589:
1588:
1538:algebraic curves
1530:
1523:
1516:
1507:
1506:
1502:
1501:
1486:Pacific J. Math.
1476:
1456:
1447:
1432:Pacific J. Math.
1429:
1419:
1387:
1351:
1338:
1334:
1326:
1305:Macbeath surface
1264:
1262:
1261:
1256:
1245:
1241:
1237:
1232:
1218:
1209:
1198:
1197:
1161:
1159:
1158:
1153:
1145:
1141:
1140:
1129:
1124:
1119:
1110:
1107:
1105:
1096:
1085:
1084:
1049:
1047:
1046:
1041:
1006:
1005:
984:
983:
962:
961:
940:
939:
906:
904:
903:
898:
886:
884:
883:
878:
866:
864:
863:
858:
846:
844:
843:
838:
822:
820:
819:
814:
803:
802:
793:
792:
780:
779:
761:
760:
709:
708:
696:
695:
683:
682:
672:
621:
619:
618:
613:
582:
580:
579:
574:
572:
571:
566:
557:
556:
501:
499:
498:
493:
463:
461:
460:
455:
446:
441:
431:
426:
404:
402:
401:
396:
373:
372:
335:It was named by
331:
329:
328:
323:
315:
314:
302:
301:
289:
288:
276:
275:
263:
262:
250:
249:
237:
236:
224:
223:
211:
210:
198:
197:
148:
146:
145:
140:
138:
137:
132:
119:projective space
111:the Bring sextic
73:
64:
50:
2160:
2159:
2155:
2154:
2153:
2151:
2150:
2149:
2135:
2134:
2133:
2124:
2096:
2087:Delta invariant
2065:
2047:
2016:
1980:
1941:Abel–Jacobi map
1922:
1896:
1892:Torelli theorem
1862:Dessin d'enfant
1842:Belyi's theorem
1828:
1814:Plücker formula
1745:
1736:Hurwitz surface
1705:
1684:
1618:
1592:Analytic theory
1584:Elliptic curves
1578:
1559:Projective line
1546:Rational curves
1540:
1534:
1427:
1409:
1342:
1341:
1331:Pacific J. Math
1327:
1323:
1318:
1291:
1278:spectral theory
1274:
1272:Spectral theory
1231:
1207:
1206:
1202:
1190:
1186:
1181:
1178:
1177:
1123:
1108:
1106:
1094:
1093:
1089:
1077:
1073:
1068:
1065:
1064:
1001:
997:
979:
975:
957:
953:
935:
931:
923:
920:
919:
892:
889:
888:
872:
869:
868:
852:
849:
848:
832:
829:
828:
798:
794:
788:
784:
775:
771:
756:
752:
704:
700:
691:
687:
678:
674:
668:
645:
642:
641:
632:Hurwitz surface
604:
601:
600:
589:
567:
562:
561:
552:
548:
546:
543:
542:
535:Riemann surface
517:
510:symmetric group
469:
466:
465:
442:
437:
427:
416:
410:
407:
406:
368:
364:
362:
359:
358:
353:
339:, p.157) after
310:
306:
297:
293:
284:
280:
271:
267:
258:
254:
245:
241:
232:
228:
219:
215:
206:
202:
193:
189:
157:
154:
153:
133:
128:
127:
125:
122:
121:
103:Bring's surface
91:
90:
89:
88:
76:
75:
74:
66:
65:
49:
12:
11:
5:
2158:
2148:
2147:
2130:
2129:
2126:
2125:
2123:
2122:
2117:
2112:
2106:
2104:
2102:Vector bundles
2098:
2097:
2095:
2094:
2089:
2084:
2079:
2074:
2069:
2063:
2057:
2055:
2049:
2048:
2046:
2045:
2040:
2035:
2030:
2024:
2022:
2018:
2017:
2015:
2014:
2009:
2004:
1999:
1994:
1988:
1986:
1982:
1981:
1979:
1978:
1973:
1968:
1963:
1958:
1953:
1948:
1943:
1937:
1935:
1928:
1924:
1923:
1921:
1920:
1915:
1910:
1904:
1902:
1898:
1897:
1895:
1894:
1889:
1884:
1879:
1874:
1869:
1864:
1859:
1854:
1849:
1844:
1838:
1836:
1830:
1829:
1827:
1826:
1821:
1816:
1811:
1806:
1801:
1796:
1791:
1786:
1781:
1776:
1771:
1766:
1761:
1755:
1753:
1747:
1746:
1744:
1743:
1738:
1733:
1728:
1723:
1717:
1715:
1711:
1710:
1707:
1706:
1704:
1703:
1698:
1692:
1690:
1686:
1685:
1683:
1682:
1677:
1672:
1667:
1662:
1657:
1652:
1647:
1642:
1637:
1632:
1626:
1624:
1620:
1619:
1617:
1616:
1611:
1606:
1601:
1595:
1593:
1586:
1580:
1579:
1577:
1576:
1571:
1569:Riemann sphere
1566:
1561:
1556:
1550:
1548:
1542:
1541:
1533:
1532:
1525:
1518:
1510:
1504:
1503:
1477:
1468:(6): 564–631,
1457:
1438:(1): 179–200,
1420:
1407:
1388:
1363:(3): 539–545,
1352:
1340:
1339:
1320:
1319:
1317:
1314:
1313:
1312:
1307:
1302:
1297:
1290:
1287:
1273:
1270:
1266:
1265:
1254:
1251:
1248:
1244:
1240:
1235:
1230:
1227:
1224:
1221:
1215:
1212:
1205:
1201:
1196:
1193:
1189:
1185:
1163:
1162:
1151:
1148:
1144:
1138:
1135:
1132:
1127:
1122:
1116:
1113:
1102:
1099:
1092:
1088:
1083:
1080:
1076:
1072:
1051:
1050:
1039:
1036:
1033:
1030:
1027:
1024:
1021:
1018:
1015:
1012:
1009:
1004:
1000:
996:
993:
990:
987:
982:
978:
974:
971:
968:
965:
960:
956:
952:
949:
946:
943:
938:
934:
930:
927:
896:
876:
856:
836:
825:
824:
812:
809:
806:
801:
797:
791:
787:
783:
778:
774:
770:
767:
764:
759:
755:
751:
748:
745:
742:
739:
736:
733:
730:
727:
724:
721:
718:
715:
712:
707:
703:
699:
694:
690:
686:
681:
677:
671:
666:
662:
659:
655:
652:
649:
611:
608:
588:
585:
570:
565:
560:
555:
551:
522:120, given by
515:
491:
488:
485:
482:
479:
476:
473:
453:
450:
445:
440:
436:
430:
425:
422:
419:
415:
394:
391:
388:
385:
382:
379:
376:
371:
367:
351:
333:
332:
321:
318:
313:
309:
305:
300:
296:
292:
287:
283:
279:
274:
270:
266:
261:
257:
253:
248:
244:
240:
235:
231:
227:
222:
218:
214:
209:
205:
201:
196:
192:
188:
185:
182:
179:
176:
173:
170:
167:
164:
161:
136:
131:
78:
77:
68:
67:
59:
58:
57:
56:
55:
9:
6:
4:
3:
2:
2157:
2146:
2143:
2142:
2140:
2121:
2118:
2116:
2113:
2111:
2108:
2107:
2105:
2103:
2099:
2093:
2090:
2088:
2085:
2083:
2080:
2078:
2075:
2073:
2070:
2068:
2066:
2059:
2058:
2056:
2054:
2053:Singularities
2050:
2044:
2041:
2039:
2036:
2034:
2031:
2029:
2026:
2025:
2023:
2019:
2013:
2010:
2008:
2005:
2003:
2000:
1998:
1995:
1993:
1990:
1989:
1987:
1983:
1977:
1974:
1972:
1969:
1967:
1964:
1962:
1959:
1957:
1954:
1952:
1949:
1947:
1944:
1942:
1939:
1938:
1936:
1932:
1929:
1925:
1919:
1916:
1914:
1911:
1909:
1906:
1905:
1903:
1901:Constructions
1899:
1893:
1890:
1888:
1885:
1883:
1880:
1878:
1875:
1873:
1872:Klein quartic
1870:
1868:
1865:
1863:
1860:
1858:
1855:
1853:
1852:Bolza surface
1850:
1848:
1847:Bring's curve
1845:
1843:
1840:
1839:
1837:
1835:
1831:
1825:
1822:
1820:
1817:
1815:
1812:
1810:
1807:
1805:
1802:
1800:
1797:
1795:
1792:
1790:
1787:
1785:
1782:
1780:
1779:Conic section
1777:
1775:
1772:
1770:
1767:
1765:
1762:
1760:
1759:AF+BG theorem
1757:
1756:
1754:
1752:
1748:
1742:
1739:
1737:
1734:
1732:
1729:
1727:
1724:
1722:
1719:
1718:
1716:
1712:
1702:
1699:
1697:
1694:
1693:
1691:
1687:
1681:
1678:
1676:
1673:
1671:
1668:
1666:
1663:
1661:
1658:
1656:
1653:
1651:
1648:
1646:
1643:
1641:
1638:
1636:
1633:
1631:
1628:
1627:
1625:
1621:
1615:
1612:
1610:
1607:
1605:
1602:
1600:
1597:
1596:
1594:
1590:
1587:
1585:
1581:
1575:
1574:Twisted cubic
1572:
1570:
1567:
1565:
1562:
1560:
1557:
1555:
1552:
1551:
1549:
1547:
1543:
1539:
1531:
1526:
1524:
1519:
1517:
1512:
1511:
1508:
1500:
1495:
1491:
1487:
1483:
1478:
1475:
1471:
1467:
1463:
1458:
1455:
1451:
1446:
1441:
1437:
1433:
1426:
1421:
1418:
1414:
1410:
1404:
1400:
1396:
1395:
1389:
1386:
1382:
1378:
1374:
1370:
1366:
1362:
1358:
1353:
1349:
1344:
1343:
1337:
1332:
1325:
1321:
1311:
1308:
1306:
1303:
1301:
1300:Klein quartic
1298:
1296:
1295:Bolza surface
1293:
1292:
1286:
1283:
1282:Bolza surface
1279:
1269:
1252:
1249:
1246:
1242:
1233:
1228:
1225:
1222:
1213:
1210:
1203:
1199:
1194:
1191:
1187:
1183:
1176:
1175:
1174:
1172:
1168:
1167:Klein quartic
1149:
1146:
1142:
1133:
1130:
1125:
1114:
1111:
1100:
1097:
1090:
1086:
1081:
1078:
1074:
1070:
1063:
1062:
1061:
1059:
1054:
1053:as expected.
1037:
1034:
1031:
1028:
1025:
1022:
1019:
1016:
1013:
1010:
1002:
998:
991:
988:
980:
976:
969:
966:
958:
954:
947:
944:
936:
932:
925:
918:
917:
916:
914:
910:
894:
874:
854:
834:
807:
804:
799:
789:
785:
781:
776:
772:
768:
762:
757:
749:
746:
740:
737:
734:
731:
728:
725:
722:
719:
716:
713:
710:
705:
701:
697:
692:
688:
684:
679:
675:
664:
660:
657:
653:
650:
640:
639:
638:
635:
633:
629:
625:
609:
606:
598:
594:
584:
568:
558:
553:
549:
540:
536:
532:
527:
525:
521:
514:
511:
507:
502:
489:
486:
483:
480:
477:
474:
471:
451:
448:
443:
438:
434:
428:
423:
420:
417:
413:
392:
389:
386:
383:
380:
377:
374:
369:
365:
357:
356:Bring quintic
350:
346:
342:
338:
319:
316:
311:
307:
303:
298:
294:
290:
285:
281:
277:
272:
268:
264:
259:
255:
251:
246:
242:
238:
233:
229:
225:
220:
216:
212:
207:
203:
199:
194:
190:
186:
183:
180:
177:
174:
171:
168:
165:
162:
159:
152:
151:
150:
134:
120:
116:
112:
108:
107:Klein quartic
104:
101:(also called
100:
99:Bring's curve
96:
86:
82:
72:
63:
47:
46:square tiling
44:and its dual
43:
39:
35:
31:
27:
23:
18:
2061:
2038:Prym variety
2012:Stable curve
2002:Hodge bundle
1992:ELSV formula
1846:
1794:Fermat curve
1751:Plane curves
1714:Higher genus
1689:Applications
1614:Modular form
1489:
1485:
1465:
1461:
1435:
1431:
1393:
1360:
1356:
1347:
1330:
1324:
1275:
1267:
1171:Schmutz 1993
1164:
1055:
1052:
826:
636:
590:
531:triple cover
528:
524:permutations
512:
503:
348:
334:
110:
102:
98:
92:
2067:singularity
1913:Polar curve
1492:: 167–182,
337:Klein (2003
95:mathematics
1908:Dual curve
1536:Topics in
1316:References
2021:Morphisms
1769:Bitangent
1377:0024-6107
1247:≈
1200:
1192:−
1147:≈
1131:−
1087:
1079:−
811:⟩
648:⟨
622:, by the
610:π
559:×
414:∑
113:) is the
2139:Category
1289:See also
593:icosagon
83:and the
38:quotient
34:its dual
26:icosagon
2092:Tacnode
2077:Crunode
1454:1154738
1417:0080930
1385:0518240
1150:4.60318
1058:systole
354:of the
117:in the
40:of the
2072:Acnode
1985:Moduli
1452:
1415:
1405:
1383:
1375:
1250:4.6245
827:where
1428:(PDF)
595:(see
520:order
115:curve
2082:Cusp
1462:GAFA
1403:ISBN
1373:ISSN
1188:cosh
1075:sinh
1056:The
504:The
464:for
20:The
1494:doi
1490:220
1470:doi
1440:doi
1436:154
1365:doi
1336:pdf
1038:240
1026:100
913:GAP
518:of
93:In
2141::
1488:,
1484:,
1464:,
1450:MR
1448:,
1434:,
1430:,
1413:MR
1411:,
1401:,
1381:MR
1379:,
1371:,
1361:18
1359:,
1071:12
1032:72
1020:64
607:12
490:3.
320:0.
109:,
97:,
2064:k
2062:A
1529:e
1522:t
1515:v
1496::
1472::
1466:3
1442::
1367::
1253:,
1243:)
1239:)
1234:3
1229:3
1226:+
1223:5
1220:(
1214:2
1211:1
1204:(
1195:1
1184:2
1143:)
1137:)
1134:1
1126:5
1121:(
1115:2
1112:1
1101:2
1098:1
1091:(
1082:1
1035:=
1029:+
1023:+
1017:+
1014:4
1011:=
1008:)
1003:2
999:6
995:(
992:2
989:+
986:)
981:2
977:5
973:(
970:4
967:+
964:)
959:2
955:4
951:(
948:4
945:+
942:)
937:2
933:1
929:(
926:4
895:t
875:s
855:r
835:e
823:,
808:e
805:=
800:2
796:)
790:2
786:r
782:s
777:3
773:r
769:s
766:(
763:=
758:4
754:)
750:s
747:r
744:(
741:=
738:t
735:s
732:t
729:s
726:=
723:t
720:r
717:t
714:r
711:=
706:2
702:t
698:=
693:2
689:s
685:=
680:5
676:r
670:|
665:t
661:,
658:s
654:,
651:r
569:2
564:Z
554:5
550:S
516:5
513:S
487:,
484:2
481:,
478:1
475:=
472:k
452:0
449:=
444:k
439:i
435:x
429:5
424:1
421:=
418:i
393:0
390:=
387:b
384:+
381:x
378:a
375:+
370:5
366:x
352:i
349:x
317:=
312:3
308:z
304:+
299:3
295:y
291:+
286:3
282:x
278:+
273:3
269:w
265:+
260:3
256:v
252:=
247:2
243:z
239:+
234:2
230:y
226:+
221:2
217:x
213:+
208:2
204:w
200:+
195:2
191:v
187:=
184:z
181:+
178:y
175:+
172:x
169:+
166:w
163:+
160:v
135:4
130:P
87:.
48:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.